个体差异是每一个孩子个性特点的体现。有的孩子无动于衷，表面上显露出勇敢，为的是隐藏失望之情；有的孩子则通过一些下意识的动作将这种失望流露出来。其他孩子则掩饰不住喜悦之情，因为他们发现自己处于一个独特的位置，这让他的同伴们非常好奇。

当3岁的孩子来到我们学校的时候，他就已经能够数二或者三了，因此，他们可以很容易地学会数数，也就是数物体的个数。有许许多多不同的方式可以达到这一目的，日常生活提供了许多机会。比如，当母亲说：“你的衣服上面掉了两颗扣子”或者“我们还要三个盘子”等等。

我最开始使用的方法是数钱。我找到一些崭新的钞票，如果可以的话我就会制作一些精美的卡片复制品了，而我曾经在伦敦的一所缺陷儿童学校里面见过。

换零钱是一种非常吸引孩子注意力的数数方法。我给孩子们1，2和4生丁的硬币，用这种方法能让孩子们学会数到10。

没有什么其他方式能够比让孩子们熟悉日常使用的硬币更加实际的了。也没有什么练习比换零钱更有用的了。正是因为他们与日常生活联系如此紧密，所以才大大引起了孩子们的兴趣。在尝试过这种以实际的方式进行数数教学后，我想试试更加系统的练习，就像在感觉训练当中所使用的木块那种教学用具，也就是我们在教授长度时所使用的10根木棒。最短的一根长10厘米，最长的是1米，中间的每根木棒相差10厘米。木棒上每10厘米的部分交替着红色和蓝色。

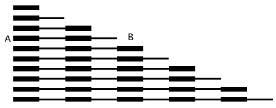
有一天，当一个孩子按照长度顺序排列这些木棒时，我们让他从最短的一根开始数红色和蓝色的记号，也就是：1；1，2；1，2，3；等等。在数每根木棒的时候都要从1开始，从A边开始。接下来，我们让他根据每根木棒上面所包含的记号数目来从短到长给每一个木棒命名，要求是从B边开始，也就是成楼梯等级的那一边开始。当孩子数最长的一根木棒时，也会得到相同的数字：1，2，3，4，5，6，7，8，9，10。如果想要知道木棒的数量，我们就从A边开始数，也是同样的结果：1，2，3，4，5，6，7，8，9，10。这正好与三角形的三边相对应。让孩子验证了自己的记数是否正确，这让他非常感兴趣，他能够进行许多遍的重复。

现在，我们再把数数练习与前面孩子认识木棒长短的感觉练习结合起来。在地毯上面将这些木棒混合起来，教师从里面拿出一根给孩子看，让孩子数上面的标记。比如说5。接下来，教师让孩子给她在长度上挨着的那一根木棒。孩子通过眼睛来进行选择，而教师将这两根木棒放在一起数上面的记号来让孩子进行验证。这种练习可以以多种方式进行重复。通过练习，孩子们学会了给每一根木棒命名。我们现在就可以称呼这些木棒为1号，2号，等等。最终，在课堂上我们可以简称为1，2，3等等。

用符号呈现的数字

在这一点上，如果孩子已经知道如何进行书写，我们就可以将这些数字用砂纸剪出来，然后贴在卡片上，这与教授字母的方法是相同的。“这是数字1”，“这是数字2”，“给我数字1”，“给我数字2”，“这是几？”孩子们就像在字母教学当中那样描画数字。

数字练习。将符号与数量联系起来。

我设计了两个盘子，每个盘子分成5部分。每部分的底面上都有一张贴着数字的卡片。第一个盘子中的数字是0，1，2，3，4，第二个是5，6，7，8，9。

练习很明确，就是要在每个部分里面放上和数字相应数量的物体。我们给孩子各种各样的物体，为的是不停变化。但主要是利用大木钉子，因为它们不容易滑落。我们在孩子面前放上这些大木钉，一个大木钉代表数字1，依此类推。当孩子完成之后，就拿给教师以检验是否正确。

0的教学。我们需要一直等到孩子们指着写有0的盘子分隔问：“我要在这里面放多少呢？”我们回答：“一个也不用放，0就是没有。”但通常情况下这还不够，有必要让孩子明白我们所说的0意味着什么。为了这一目的，我们利用了一个让孩子非常放松的小游戏。我站在他们中间，然后转向其中一个已经进行过这一练习的孩子说：“亲爱的，过来，到我这里来0次。”孩子们几乎总是到我这里来，然后又跑回到自己的位置。“可是，我的孩子，你来过了1次，而我告诉你的是来0次。”接下来，孩子就想知道原因了。“可是我应该怎么做呢？”“什么也不做，0就是什么也没有。”“可是我该怎样去做什么都没有呢？”“你不要做任何事情，你必须静静地站在那里。你不应该过来。0次，就是一次也没有。”我一直重复这一练习直到孩子们理解。当我让他们到我这里来0次或者是吻我0下的时候，他们对于保持安静感到非常好笑。他们自己经常喊道：“0就是什么都没有！0就是什么都没有！”

数字记忆练习

当孩子们认识书写的数字，并且知道这些数字所代表的数值的时候，我就进行如下练习：

我从旧日历上面将数字剪下来，然后贴在卡片上，叠好放在盒子里面。孩子们抽出卡片回到座位上，在座位上打开卡片，看完后再将卡片叠好，并且不让别人知道。接下来，可以让这些孩子们（一般说来很自然的是班上年龄最大的孩子们）一个接一个或者分成小组，来到教师桌子边上，桌子上面放有各种各样的小物体。每一个孩子都根据自己卡片上的数字来选择相应的物体数目。而与此同时，孩子要将自己的卡片也放在物体边上，当然是叠好的以保密。在这一过程当中，孩子们不但要在来回走动的过程里面，而且要在选取物体一个一个数的时候，一定牢牢记住自己的数字。在此，教师就可以对每一个体的数字记忆差别进行有趣的观察了。

当孩子们拿好了物体之后，就回到自己的桌子上进行摆放。他们要将物体摆放成相等的两列。如果数字不是偶数的话，那孩子们就要把最后一个落单的物体放在这两列最下面的正中间，就像图表所显示的那样：十字代表物体，小圆圈代表写有数字的叠好的卡片。在排列好物体之后，孩子们就等待着教师的检验。教师来到桌子前面，打开卡片，读出数字，然后数物体的数目。

当我们一开始进行这一游戏的时候，孩子们经常要比卡片上所要求的数字多拿一些，这并不是因为他们记不住数字，而是因为他们想要拥有最多的物体，这是人类贪婪本能的一种体现，而这对那些原始而没有受过教育的人来说是非常普遍的。这时教师就要向孩子们解释，告诉他们就是把所有的都拿过来也没有用，因为这一游戏的要点就在于拿取卡片上所要求数目的物体。

慢慢的，孩子们开始明白了这一概念，但是并不像一个人想象的那么容易。这是一种自我否定的努力，这种否定要求孩子们将自己限制在一定范围之内。比如，当他看见别的孩子拿了许多东西的时候，自己应当按要求只拿两个。

因此，我认为这一游戏不但是一种数字练习，而且更是一种意志力的练习。特别是那个抽到0的孩子，他不应该拿任何东西，而同时却只能眼睁睁地看着其他同伴自由的选取物体。有许多次，0落到了数数非常好的孩子手里面，他们本应该在拿物体和将这些物体摆放整齐并且等待教师检验的时候感到巨大的快乐，可是这次却不能了。

研究那些抽到0的孩子们的面部表情是最有趣的事情了。个体差异是每一个孩子个性特点的体现。有的孩子无动于衷，表面上显露出勇敢，为的是隐藏失望之情；有的孩子则通过一些下意识的动作将这种失望流露出来。其他的孩子则掩饰不住喜悦之情，因为他们发现自己处于一个独特的位置，这让他的同伴们非常好奇。有的孩子以一种渴望，几乎是嫉妒的目光打量着其他同伴的每一个动作，而另外有一些孩子表现出立即接受了这种情况。当在进行检验的时候，那些拿着0的孩子的表情是最有趣的了。“你为什么什么东西都没有拿呢？”“我抽到了0”，“是0”。这些话都很普通，但是孩子们的面部表情以及说话的腔调表现出了各种不同的情绪。

实际上，很少有人在解释的时候流露出高兴的表情，大多数都是不高兴或者是无可奈何。

所以，我们对这一游戏的意义进行了说明：“如果抽到0，那么想要保守秘密就非常难了，这是最难的。”这样过了一会，保持安静这一难题吸引了孩子们，当他们打开写有0的卡片时，我们可以看到他们还是可以保守秘密的。

1～20的加减乘除法

我们在第一次教授算术运算时所使用的教学用具与在数数时所用的是相同的。也就是那些根据长度不同进行着色的木棒，这里面还包含了十进制的最初概念。

正如我所说过的，这些木棒根据所代表的数字进行称呼：1，2，3，等等。他们按照长度进行排列，而这同时也是在按照数字进行排列。

第一个练习包括用木棒组成10。最简单的方法是将从1开始的木棒按顺序放到从9向下的木棒边上。我们在进行这一步骤的同时可以这样指挥：“把1拿起来，然后放到9边上；把2拿起来，放到8边上；把3拿起来，放到7边上；把4拿起来，放到6边上。”通过这种方式，我们组成了四组等于10的木棒。还剩下5，我们将5转一下头，就会发现从这头开始到那一边与其他的10是相等的，就明确了5的2倍是10这样一个事实。

重复这一练习，孩子们慢慢就学会了更加专业的语言：9加1等于10；8加2等于10；7加3等于10；6加4等于10，对于剩下的5来说，5乘以2等于10。最后，如果孩子们能够进行书写，我们就教给他们加号，减号和乘号。下面就是我们在一个小朋友整齐的笔记本上看到的：

9＋1＝10

8＋2＝10

7＋3＝10

6＋4＝10

当所有这些孩子们都已经学会，并且对在纸上书写表现出极大快乐的时候，我们就要将孩子们的注意力转移到将那些已经形成10的数字组合上来，将这些数字分开然后放回到原始的位置上。在最后一组10当中，我们拿走了4，剩下6；接下来我们拿走3剩下7；依次，我们拿走2剩下8，拿走1剩下9。为了清楚的说明这些，我们可以说：“比10少4等于6；比10少3等于7；比10少2等于8；比10少1等于9。”

在轮到最后剩下的5时，我们可以说10的一半是5。通过将长木棒截成两段，也就是将10分成两份，我们就得到了5。10除以2等于5。有关这一过程的记录如下：

10－4＝6　　　　　　　　

10－3＝7　　　　10÷2＝5

10－2＝8　　　　　　　　

10－1＝9　　　　　　　　

一旦孩子们掌握了这一练习，他们就能自觉的举一反三。“我们可以通过两种方法得到3，对吗？”在2后面写上1，2＋1＝3。我们也可以用两根木棒相拼来与木棒4相等对吗？3＋1＝4，4－3＝1，4－1＝3。木棒2和木棒4之间的关系与木棒5和木棒10之间的关系是相同的，也就是说我们将木棒2翻转一下就会发现4里面正好包含着两个2，即4÷2＝2；2×2＝4。我们来看看另外一个问题：进行这同一个游戏，我们可以使用多少木棒呢？我们可以用3和6，4和8，也就是：

2×2＝4　　3×2＝6　　4×2＝8　　5×2＝10

10÷2＝5　　8÷2＝4　　6÷2＝3　　4÷2＝2

在这里我们发现用来进行数字记忆的正方体可以提供帮助：

2　　　4　　　6　　　8　　　10

按照这种排列，可以立刻看出那些数字能够被2整除——所有这些数字在正方体的底下均没有一个单独的数字。这些数字都是偶数，因为它们能够两两成对排列，并且可以被2整除。数每一列当中的数目我们就得到了商。而为了还原为原始数字，我们只需要将这两列进行重组，也就是2×3＝6。所有这些对于5岁的孩子来说并不困难。

这种重复练习很快就变得非常单调，但是练习可以很容易的进行变化。我们把这套木棒拿过来，不再将木棒1放在木棒9后面，而是放在木棒10后面。同理，我们将木棒2放在木棒9后面，木棒3放在木棒8后面。通过这种方式，我们让木棒要比10长，这些长度分别是11，12，13，等等，直到20。木棒也可以用来表示这些数字。

因为我们已经学过10以内的运算，所以在进行20以内的运算时就没有困难了。唯一的困难就在十进制，而这需要一定的专门课程。

十进制课程：大于10的算术运算

必要的教学用具包括一些正方形卡片，在卡片上面数字10用大号字体印着。我们还需要一些长方形的卡片，这些长方形卡片恰巧是正方形卡片的一半，包含着从1到9的单个数字。我们把这些数字排成一条直线：1，2，3，4，5，6，7，8，9，10。我们从1开始，这里的1就像是木棒教学当中的10，它超过了9。我们沿着数字阶梯一直数到9，因为再数就没有数字了，我们再次从1开始。但是这里的1要比一开始的那个1高一个等级，为了进行区分，我们将这个1放在0边上，这样就是10。接下来我们用写有数字的长方形卡片按顺序将0覆盖住，就得到了：11，12，13，14，15，16，17，18，19。通过将木棒1，木棒2，木棒3直到木棒9，分别与木棒10相加我们就得到了这些数字，最终我们得到了一个非常长的木棒，当我们数上面交错的红色和蓝色时，就得到了19。

接着，教师可以给孩子们看卡片，比如数字16，这时教师可以在木棒10后面放上木棒6。然后，教师将写有6的卡片拿走，换成数字8的卡片，与此同时，孩子们将木棒6拿走，然后放上木棒8，组成18。所有这些动作可以进行如下记录：10＋6＝16；10＋8＝18等等。对于减法我们也采用相同的方法。

当孩子们对数字有了一个清晰概念的时候，我们要做一个结合，就像在图A和图B上面所表明的那样。

在左面的A当中，我们在第二个10的0上面用写有数字1的卡片进行覆盖，以次类推。这样，第一个10保持不变，而右边的数字则是从1到9。

在卡片B当中，应用要更复杂一些。上面的数字每个相差10。

这样几乎所有的孩子都能够数到100，因为这是为了满足他们在学习时的好奇心。

我认为这一阶段的教学没有必要进行深入的说明。每一位教师都能使算术运算产生变化，并且利用一些孩子们容易处理的物体。