上次说到，在微粒与波动的第一次交锋中，以牛顿为首的微粒说战胜了波动说，取得了在物理界被普遍公认的地位。

转眼间，近一个世纪过去了。牛顿体系的地位已经是如此崇高，令人不禁有一种目眩的感觉。而他所提倡的光是一种粒子的观念也已经是如此地深入人心，以致人们几乎都忘了当年它那对手的存在。

然而1773年6月13日，英国米尔沃顿（Milverton）的一个教徒的家庭里诞生了一个男孩，取名为托马斯•杨（Thomas Young）。这个未来反叛派领袖的成长史是一个典型的天才历程：他2岁的时候就能够阅读各种经典，6岁时开始学习拉丁文，14岁就用拉丁文写过一篇自传，到了16岁时他已经能够说10种语言。在语言上的天才使得杨日后得以破译埃及罗塞塔碑上的许多神秘的古埃及象形文字，并为埃及学的正式创立作了突出的贡献（当然，埃及学的主要奠基者还是商博良）。不过对于我们的史话来说更为重要的是，杨对自然科学也产生了浓厚的兴趣，他学习了牛顿的《数学原理》以及拉瓦锡的《化学纲要》等科学著作，为将来的成就打下了坚实的基础。

杨19岁的时候，受到他那当医生的叔父的影响，决定去伦敦学习医学。在以后的日子里，他先后去了爱丁堡和哥廷根大学攻读，最后还是回到剑桥的伊曼纽尔学院终结他的学业。在他还是学生的时候，杨研究了人体上眼睛的构造，开始接触到了光学上的一些基本问题，并最终形成了他那光是波动的想法。杨的这个认识，是来源于波动中所谓的“干涉”现象。

我们都知道，普通的物质是具有累加性的，一滴水加上一滴水一定是两滴水，而不会一起消失。但是波动就不同了，一列普通的波，它有着波的高峰和波的谷底，如果两列波相遇，当它们正好都处在高峰时，那么叠加起来的这个波就会达到两倍的峰值，如果都处在低谷时，叠加的结果就会是两倍深的谷底等等。但是，如果正好一列波在它的高峰，另外一列波在它的谷底呢？

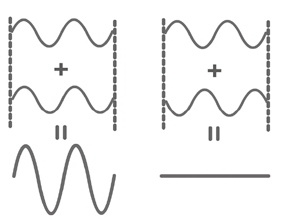
答案是它们会互相抵消。如果两列波在这样的情况下相遇（物理上叫做“反相”），那么在它们重叠的地方，将会波平如镜，既没有高峰，也没有谷底。这就像一个人把你往左边拉，另一个人用相同的力气把你往右边拉，结果是你会站在原地不动。

托马斯•杨在研究牛顿环的明暗条纹的时候，被这个关于波动的想法给深深打动了。为什么会形成一明一暗的条纹呢？一个思想渐渐地在杨的脑海里成型：用波来解释不是很简单吗？明亮的地方，那是因为两道光正好是“同相”的，它们的波峰和波谷正好相互增强，结果造成了两倍光亮的效果（就好像有两个人同时在左边或者右边拉你）；而黑暗的那些条纹，则一定是两道光处于“反相”，它们的波峰波谷相对，正好互相抵消了（就好像两个人同时在两边拉你）。这一大胆而富于想象的见解使杨激动不已，他马上着手进行了一系列的实验，并于1801年和1803年分别发表论文报告，阐述了如何用光波的干涉效应来解释牛顿环和衍射现象。甚至通过他的实验数据，计算出了光的波长应该在1/36000至1/60000英寸之间。

在1807年，杨总结出版了他的《自然哲学讲义》，里面综合整理了他在光学方面的工作，并第一次描述了他那个名扬四海的实验：光的双缝干涉。后来的历史证明，这个实验完全可以跻身于物理学史上最经典的前五个实验之列。而在今天，它更是理所当然地出现在每一本中学物理的教科书上。

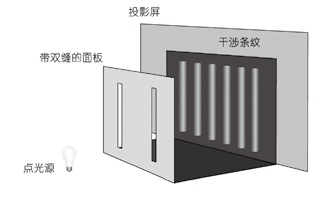
杨的实验手段极其简单：把一支蜡烛放在一张开了一个小孔的纸前面，这样就形成了一个点光源（从一个点发出的光源）。现在在纸后面再放一张纸，不同的是第二张纸上开了两道平行的狭缝。从小孔中射出的光穿过两道狭缝投到屏幕上，就会形成一系列明、暗交替的条纹，这就是现在众人皆知的干涉条纹[我在这里描述的是较大众化的版本。杨最早的实验是用一张卡片把光束分割成两半以达到同样效果，实际上并未用到“双缝”。]。

杨的著作点燃了革命的导火索，物理史上的“第二次波粒战争”开始了。波动方面军在经过了百年的沉寂之后，终于又回到了历史舞台上来。但是它当时的日子并不是好过的，在微粒大军仍然一统天下的年代，波动的士兵们衣衫褴褛，缺少后援，只能靠游击战来引起人们对它的注意。杨的论文开始受尽了权威们的嘲笑和讽刺，被攻击为“荒唐”和“不合逻辑”，在近20年间竟然无人问津。杨为了反驳专门撰写了论文，但是却无处发表，只好印成小册子，但是据说发行后“只卖出了一本”。

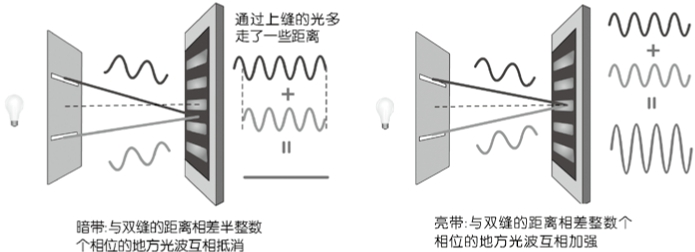
不过，虽然高傲的微粒仍然沉醉在牛顿时代的光荣之中，一开始并不把起义的波动叛乱分子放在眼里。但他们很快就发现，这些反叛者虽然人数不怎么多，服装并不那么整齐，但是他们的武器却今非昔比。在受到了几次沉重的打击后，干涉条纹这门波动大炮的杀伤力终于惊动整个微粒军团。这个简单巧妙的实验所揭示出来的现象证据确凿，几乎无法反驳。无论微粒怎么样努力，也无法躲开对手的无情轰炸：它就是难以说明两道光叠加在一起怎么会反而造成黑暗。而波动的理由却是简单而直接的：两条缝距离屏幕上某点的距离会有所不同。当这个距离差是波长的整数倍时，两列光波正好互相加强，就在此形成亮带。反之，当距离差刚好造成半个波长的相位差时，两列波就正好互相抵消，这个地方就变成暗带。理论计算出的明暗条纹距离和实验值分毫不差。

在节节败退后，微粒终于发现自己无法抵挡对方的进攻，于是它采取了以攻代守的战略。许多对波动说不利的实验证据被提出来以证明波动说的矛盾，其中最为知名的就是马吕斯（Étienne Louis Malus）在1809年发现的偏振现象，这一现象和已知的波动论有抵触的地方。两大对手开始相持不下，但是各自都没有放弃自己获胜的信心。杨在给马吕斯的信里说：“……您的实验只是证明了我的理论有不足之处，但没有证明它是虚假的。”

决定性的时刻在1819年到来了。最后的决战起源于1818年法国科学院的一个悬赏征文竞赛，竞赛的题目是利用精密的实验确定光的衍射效应以及推导光线通过物体附近时的运动情况。竞赛评委会由许多知名科学家组成，这其中包括比奥（J. B. Biot）、拉普拉斯（Pierre Simon de Laplace）和泊松（S. D. Poission），都是积极的微粒说拥护者。从这个评委会的本意来说，他们或许是希望通过微粒说的理论来解释光的衍射以及运动，以打击波动理论。

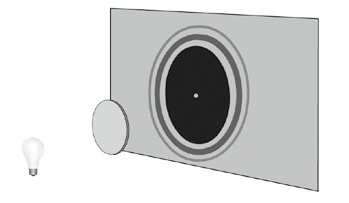
但是戏剧性的情况出现了：一个不知名的法国年轻工程师——菲涅耳（Augustin Fresnel，当时他才31岁）向组委会提交了一篇论文。在这篇论文里，菲涅耳采用了光是一种波动的观点，并以严密的数学推理，极为圆满地解释了光的衍射问题。他的体系洋洋洒洒，天衣无缝，完美无缺，令委员会成员为之深深惊叹。泊松并不相信这一结论，对它进行了仔细的审查，结果发现当把这个理论应用于圆盘衍射的时候，在阴影中间将会出现一个亮斑。这在泊松看来是十分荒谬的，影子中间怎么会出现亮斑呢？这差点使得菲涅耳的论文中途夭折。但菲涅耳的同事，评委之一的阿拉果（François Arago）在关键时刻坚持要进行实验检测，结果发现真的有一个亮点如同奇迹一般地出现在圆盘阴影的正中心，位置亮度和理论符合得相当完美。

菲涅耳理论的这个胜利成了第二次波粒战争的决定性事件。他获得了那一届的科学奖（Grand Prix），同时一跃成为了可以和牛顿、惠更斯比肩的光学界的传奇人物。圆盘阴影正中的亮点（后来被相当误导性地称作“泊松亮斑”）成了波动军手中威力不下于干涉条纹的重武器，给了微粒势力以致命的一击，起义者的烽火很快就燃遍了光学的所有领域。但是，光的偏振问题却仍旧没有得到解决，微粒依然躲在这个掩体后面负隅顽抗，不停地向波动开火。为此，菲涅耳不久后又作出了一个石破天惊的决定：他革命性地假设光是一种横波（也就是类似水波那样，振子作相对传播方向垂直运动的波），而不像从胡克以来所一直认为的那样，是一种纵波（类似弹簧波，振子作相对传播方向水平运动的波）。1821年，菲涅耳发表了题为《关于偏振光线的相互作用》的论文，用横波理论成功地解释了偏振现象，攻克了战役中一个最难以征服的据点。

大反攻的日子已经到来。微粒说在偏振问题上失守后，已经是捉襟见肘，节节溃退。到了19世纪中期，微粒说挽回战局的唯一希望就是光速在水中的测定结果了。因为根据粒子论，这个速度应该比真空中的光速要快，而根据波动论，这个速度则应该比真空中要慢才对。

然而不幸的微粒军团终于在1819年的莫斯科严冬之后，又于1850年迎来了它的滑铁卢。这一年的5月6日，傅科（Jean-Bernard-Léon Foucault，他后来以“傅科摆”实验而闻名）向法国科学院提交了他关于光速测量实验的报告。在准确地得出光在真空中的速度之后，他也进行了水中光速的测量，发现这个值小于真空中的速度，只有前者的3/4。这一结果彻底宣判了微粒说的死刑，波动论终于在100多年后革命成功，推翻了微粒王朝，登上了物理学统治地位的宝座。在胜利者盛大的加冕典礼中，第二次波粒战争随着微粒的战败而尘埃落定。

但菲涅耳的横波理论却留给波动一个尖锐的难题，就是以太的问题。光是一种横波的事实已经十分清楚，它传播的速度也得到了精确测量，这个数值达到了30万公里/秒，是一个惊人的高速。通过传统的波动论，我们不难得出它的传播媒介的性质：这种媒介必定是一种异常坚硬的固体！它比最硬的物质金刚石还要硬上不知多少倍。然而事实是从来就没有任何人能够看到或者摸到这种“以太”，也没有实验测定到它的存在。星光穿越几亿亿公里的以太来到地球，然而这些坚硬无比的以太却不能阻挡任何一颗行星或者彗星的运动，哪怕是灰尘也不行！

波动对此的解释是以太是一种刚性的粒子，但是它却是如此稀薄，以致物质在穿过它们时几乎完全不受到任何阻力，“就像风穿过一小片丛林”（托马斯•杨语）。以太在真空中也是绝对静止的，只有在透明物体中，可以部分地被拖曳（菲涅耳的部分拖曳假说）。

这个观点其实是十分牵强的，但是波动说并没有为此困惑多久，因为更加激动人心的胜利很快就到来了。伟大的麦克斯韦于1856、1861和1865年发表了三篇关于电磁理论的论文，这是一个开天辟地的工作，它在牛顿力学的大厦上又完整地建立起了另一座巨构，而且其辉煌灿烂绝不亚于前者。麦克斯韦的理论预言，光其实只是电磁波的一种。这段文字是他在1861年的第二篇论文《论物理力线》里面特地用斜体字写下的。而我们在本章的一开始已经看到，这个预言是怎样由赫兹在1887年用实验予以了证实。波动说突然发现，它已经不仅仅是光领域的统治者，而是业已成为了整个电磁王国的最高司令官。波动的光辉到达了顶点，只要站在大地上，它的力量就像古希腊神话中的巨人那样，是无穷无尽而不可战胜的。而它所依靠的大地，就是麦克斯韦不朽的电磁理论。

饭后闲话：阿拉果的遗憾

阿拉果一向是光波动说的捍卫者，他和菲涅耳在光学上其实是长期合作的。菲涅耳的参赛得到了阿拉果的热情鼓励，而菲涅耳关于光是横波的思想，最初也是来源于托马斯•杨写给阿拉果的一封信。他和菲涅耳共同作出了对于相互垂直的两束偏振光线的相干性的研究，明确了来自同一光源但偏振面相互垂直的两支光束，不能发生干涉。但在双折射和偏振现象上，菲涅耳显然更具有勇气和革命精神。在两人完成了《关于偏振光线的相互作用》这篇论文后，菲涅耳指出只有假设光是一种横波，才能完满地解释这些现象，并给出了推导。然而阿拉果对此抱有怀疑态度，认为菲涅耳走得太远了。他坦率地向菲涅耳表示，自己没有勇气发表这个观点，并拒绝在这部分论文后面署上自己的名字。于是最终菲涅耳以自己一个人的名义提交了这部分内容，引起了科学界的震动。

这大概是阿拉果一生中最大的遗憾，他本有机会和菲涅耳一样成为在科学史上大名鼎鼎的人物。当时的菲涅耳虽然崭露头角，毕竟还是无名小辈，而他在学界却已经声名显赫，被选入法兰西研究院时，得票甚至超过了著名的泊松。其实在光波动说方面，阿拉果做出了许多杰出的贡献，不在菲涅耳之下，许多还是两人互相启发而致的。在菲涅耳面临泊松的质问时，阿拉果仍然站在了菲涅耳一边，正是他的实验证实了泊松光斑的存在，使得波动说取得了最后的胜利。但关键时候的迟疑，却最终使得他失去了“物理光学之父”的称号。这一桂冠如今戴在菲涅耳的头上。