物理学，海森堡坚定地想，应当有一个坚固的基础，它只能够从一些直接可以被实验观察和检验的东西出发。一个物理学家应当始终坚持严格的经验主义，而不是想象一些图像来作为理论的基础。玻尔理论的毛病，恰恰就出在这上面。

我们再来回顾一下玻尔理论说了些什么。它说，原子中的电子绕着某些特定的轨道以一定的频率运行，并时不时地从一个轨道跃迁到另一个轨道上去。每个电子轨道都代表一个特定的能级，因此当这种跃迁发生的时候，电子就按照量子化的方式吸收或者发射能量，其大小等于两个轨道之间的能量差。

嗯，听起来不错，而且这个模型在许多情况下的确管用。但是，海森堡开始问自己。一个电子的“轨道”，它究竟是什么东西？有任何实验能够让我们看到电子的确绕着某个轨道运转吗？有任何实验可以确实地测出一个轨道的能量，或者它离开原子核的实际距离吗？诚然，轨道的图景生动而鲜明，为人们所熟悉，可以类比于行星的运行轨道，但是和行星不同，有没有任何法子让人们真正地看到电子的这么一个“轨道”，并实际测量一个轨道所代表的“能量”呢？没有法子，电子的轨道，还有它绕着轨道的运转频率，都不是能够实际观察到的，那么人们是怎么得出这些概念并在此之上建立起原子模型的呢？

我们回想一下前面史话的有关部分，玻尔模型的建立有着氢原子光谱的支持。每一条光谱线都有一种特定的频率，而由量子公式E₁-E₂=hv，我们知道这是电子在两个能级之间跃迁的结果。但是，海森堡争辩道，你这还是没有解决我的疑问，没有实际的观测可以证明某一个轨道所代表的“能级”是什么。每一条频率为ν的光谱线，只代表两个“能级”之间的“能量差”。我们直接观察到的，既不是E₁，也不是E₂，而是E₁-E₂！换句话说，只有“能级差”或者“轨道差”是可以被直接观察到的而“能级”和“轨道”却不是。

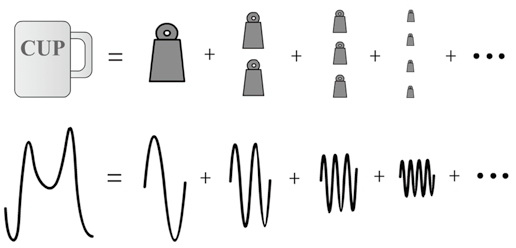
现在，我们必须从头审视一下传统的模型，看看问题究竟出在何处。在经典力学中，一个周期性的振动可以用数学方法分解成为一系列简谐振动的叠加，这个方法叫做傅里叶级数展开（Fourier series），它在工程上有着极为重要的应用。无论怎样奇形怪状的函数，只要它的频率为ν，我们便可以把它写成一系列的频率为nν的正弦波的叠加。这就好比用天平称重量，只要我们有一套尺寸非常齐备的砝码，我们就可以用它们称出任意重量来，精确度达到无限。好比说，假设我们的工具箱里有n种砝码，每种对应的重量单位是10ⁿ克，那么显然有：

123.456……克 ＝ 1个100克+2个10克+3个1克+4个0.1克+5个0.01克+6个0.001克……的砝码

我们的傅里叶展开是一个意思，只不过把那n个重量为10ⁿ克的标准砝码理解为频率为nν的标准正弦波而已。这样一来，任何振动也都可以表示为若干个强度为Fn，频率为nν的“砝码”的叠加[为了简便起见，我们用的是指数形式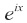，包含正弦波 cos（x）+isin（x）。如果你是大学理科生，应该能够理解，不然只好罚你回去温习大一的功课。对于数学没兴趣的读者而言，则大可不必理会其中的细节。]：

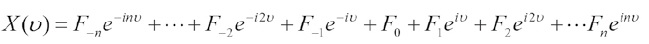
回到玻尔模型中来。一个电子的运动方程是怎样的呢？它应该是所谓的“能级”和时间的函数，在一个特定的能级X上，电子以频率v_x 作周期运动，这使得我们刚学到的傅里叶分析有了用武之地，可以将其展开为无限个频率为nv_x 的简谐振动的叠加。玻尔的理论正是用这种经典手法来处理的：简单而言，一个能级对应于一个特定的频率ν。

但是，海森堡现在开始对此表示怀疑。一个绝对的“能级”或者“频率”，有谁曾经观察到过这些物理量吗？没有，我们唯一可以观察的只有电子在能级之间跃迁时的“能级差”。如果说一种物理量无论如何也观察不到，那么我们凭什么把它高高供奉，当作理论的基础呢？玻尔的原子大厦就是建筑在这种流沙之上，所以终于摇摇欲坠。要拯救物理学，现在只有彻底抛弃那些幻想和猜臆，重新一步一个脚印地去寻找一块坚实的地基才行。

一种不可言的神秘的氛围正在四周不断升温蔓延，让我们虔心地祈祷，看看将会发生些什么怪事。如果单独的能级X无法观测，只有“能级差”可以，那么频率必然要表示为两个能级X和Y的函数。我们用傅立叶级数展开的，不再是nv_x，而必须写成nv_{x, y}。可是，等等, nv_{x, y}是个什么东西呢？它竟然有两个坐标，这是一张二维的表格！突然之间，Matrix这个怪物在我们的宇宙里妖诡地铺展开来，像一张无边无际的网，把整个时间和空间都网罗在其中。

各位可能有点不知所措。为了进一步让大家明白问题所在，我们还是来打个简单的比方：如今大城市的巴士大多都是无人售票的统一收费，上车就付2块钱。不过七八十年代出生的人都应该记得，小时候那阵，车费是按照乘坐距离的长短来计价的（所以需要售票员）。不管你从哪个站上车，坐得越远车票就相对越贵。比如说在上海，我从徐家汇上车，那么坐到淮海路可能只要3分钱，而到人民广场大概就要5分，到外滩就要7分，如果一直坐到虹口体育场，也许就得花上1毛钱。那真是一段令人怀念的golden old days（黄金时代）。

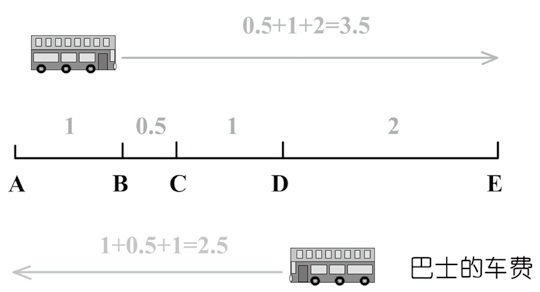
言归正传，让我们假设有一班巴士从A站出发，经过BCD三站到达E这个终点站。这个车的收费沿用了我们怀旧时代的老传统，不是上车一律给2块钱，而是根据起点和终点来单独计费。我们不妨订一个收费标准：A站和B站之间是1块钱，B站和C站靠得比较近，0.5元。C站和D站之间还是1块钱，而D站和E站离得远，2块钱。这样一来车费就容易计算了，比如我从B站上车到E站，那么我就应该给0.5+1+2=3.5元作为车费。反过来，如果我从D站上车到A站，那么道理是一样的：1+0.5+1=2.5元。

现在玻尔和海森堡分别被叫来写一个关于车费的说明贴在车子里让人参考。玻尔欣然同意了，他说：这个问题很简单，车费问题实际上就是两个站之间的距离问题，我们只要把每一个站的位置状况写出来，那么乘客们就能够一目了然了。于是他就假设，A站的坐标是0，从而推出：B站的坐标是1，C站的坐标是1.5，D站的坐标是2.5，而E站的坐标是4.5。这就行了，玻尔说，车费就是起点站的坐标减掉终点站的坐标的绝对值，我们的“坐标”，实际上可以看成一种“车费能级”，所有的情况都完全可以包含在下面这个表格里：

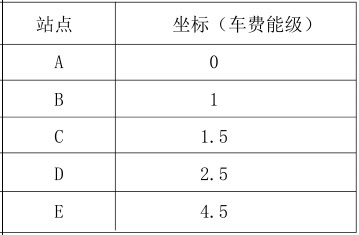
这便是一种经典的解法，每一个车站都被假设具有某种绝对的“车费能级”，就像原子中电子的每个轨道都被假设具有某种特定的能级一样。所有的车费，不管是从哪个站到哪个站，都可以用这个单一的变量来解决，这是一个一维的传统表格，完全可以表达为一个普通的公式。这也是所有物理问题的传统解法。

现在，海森堡说话了。不对，海森堡争辩说，这个思路有一个根本性的错误，那就是，作为一个乘客来说，他完全无法意识，也根本不可能观察到某个车站的“绝对坐标”是什么。比如我从C站乘车到D站，无论怎么样我也无法观察到“C站的坐标是1.5”，或者“D站的坐标是2.5”这个结论。作为我——乘客来说，我所能唯一观察和体会到的，就是“从C站到达D站要花1块钱”，这才是最确凿，最坚实的东西。我们的车费规则，只能以这样的事实为基础，而不是不可观察的所谓“坐标”，或者“能级”。

那么，怎样才能仅仅从这些可以观察的事实上去建立我们的车费规则呢？海森堡说：

传统的那个一维表格已经不适用了，我们需要一种新类型的表格，像下面这样的：

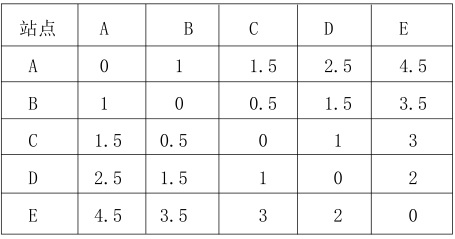
这里面，横坐标是起点站，纵坐标是终点站。现在这张表格里的每一个数字都是实实在在可以观测和检验的了。比如第一行第三列的那个1.5，它的横坐标是A，表明从A站出发。它的纵坐标是C，表明到C站下车。那么，只要某个乘客真正从A站坐到了C站，他就可以证实这个数字是正确的：这个旅途的确需要1.5块车费。

海森堡的表格和玻尔的不同，它没有做任何假设和推论，不包含任何不可观察的数据。但作为代价，它采纳了一种二维的庞大结构，每个数据都要用横坐标和纵坐标两个变量来表示。正如我们不能用v_x，而必须用nv_x来表示电子频率一样。更关键的是，海森堡争辩说，所有的物理规则，也要按照这种表格的方式来改写。我们已经有了经典的动力学方程，现在，我们必须全部把它们按照量子的方式改写成某种表格方程。许多传统的物理变量，现在都要看成是一些独立的矩阵来处理。在玻尔和索末菲的旧原子模型里，用傅里叶级数展开的电子运动方程，也必须用矩阵重新加工，把不可观察的泥沙剔除出去，注入混凝土的坚实基础——可实际检验的物理量。

但是难题来了，我们现在有一个变量p，代表电子的动量；还有一个变量q，代表电子的位置。本来，这是两个经典变量，我们应该把它们相乘，大家都没有对此表示任何疑问。可现在，海森堡把它们改成了矩阵的表格形式，这就给我们的运算带来了麻烦。p和q变成了两个“表格”！请问，你如何把两个“表格”乘起来呢？

或者我们不妨先问自己这样一个问题：把两个表格乘起来，这代表了什么意义呢？

为了容易理解，我想让大家做一道小学生水平的数学练习：乘法运算。只不过这次乘的不是普通的数字，而是两张表格：I和Ⅱ。它们的内容见下：

I：

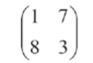
Ⅱ：

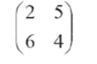
那么，各位同学，I×Ⅱ等于几？这道题就当是今天的回家作业，现在我们暂时下课。

饭后闲话：男孩物理学

1925年，当海森堡做出他那突破性的贡献的时候，他刚刚24岁。尽管在物理上有着极为惊人的天才，但海森堡在别的方面无疑还只是一个稚气未脱的大孩子。他兴致勃勃地跟着青年团去各地旅行，在哥本哈根逗留期间，他抽空去巴伐利亚滑雪，结果摔伤了膝盖，躺了好几个礼拜。在山谷田野间畅游的时候，他高兴得不能自已，甚至说“我连一秒钟的物理都不愿想了”。这种政治和为人处世上的天真在后来的岁月里也一再地显露出来。

量子论的发展几乎就是年轻人的天下。爱因斯坦1905年提出光量子假说的时候，也才26岁。玻尔1913年提出他的原子结构的时候，28岁。德布罗意1923年提出相波的时候，31岁（还应该考虑到他并非科班出身）。而1925年，当量子力学在海森堡的手里得到突破的时候，后来在历史上闪闪发光的那些主要人物也几乎都和海森堡一样年轻：泡利25岁，狄拉克23岁，乌仑贝克25岁，古兹密特23岁，约尔当23岁。和他们比起来，36岁的薛定谔和43岁的波恩简直算是老爷爷了。量子力学被人们戏称为“男孩物理学”，波恩在哥廷根的理论班，也被人叫做“波恩幼儿园”。

不过，这只说明量子论的锐气和朝气。在那个神话般的年代，象征了科学永远不知畏惧的前进步伐，开创出一个前所未有的大时代来。“男孩物理学”这个带有传奇色彩的名词，也将成为科学史上一段永远惹人遐想的佳话吧!