好了各位同学，我们又见面了。上次我们布置了一道练习题，不知大家有没有按时完成呢？不管怎样都好，现在我们一起来把它的答案求出来。

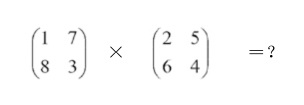
出于寓教于乐的目的，我们还是承接上一节，用比喻的方式来解答这个问题。大家还记得，每张表格代表了一种海森堡式的车费表，那么现在我们的I和Ⅱ就分别成了两条路线的旅游巴士，在两个城市之间来往，只不过收费有所不同而已。我们把它们称为巴士I号线和巴士Ⅱ号线。为了再形象化一点，我们假设这两个城市是隔着罗湖桥比邻的深圳和香港。

这样的话，我们的表格就有了具体的现实意义。如前面已经说明的那样，表的横坐标是出发站，纵坐标是终点站。所以对于巴士I号线来说，在深圳市内游玩需要1块车费，从深圳出发到香港则要7块钱。反过来，从香港出发回深圳要8块钱，而在香港市内观光则需3块[数字只是为了简便而用来举例。事实上当然没这么便宜，换成美金差不多。]。Ⅱ号表格里的数字与此类似。

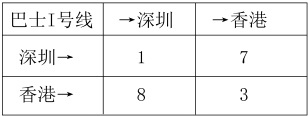
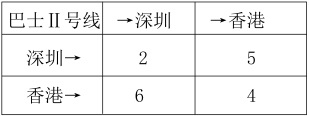
好吧，到目前为止一切都不错，可是，这到底有什么意思呢？I×Ⅱ到底是多少呢？这种运算代表什么意义呢？和我们的巴士旅游线又有什么关系呢？暂且不急，让我们一步一步地来解决这个问题。

首先要把握大方向。I是一个2×2的表格，Ⅱ也是一个2×2的表格。那么，我们有理由去猜测，它们的乘积应该也是一个2×2的表格。

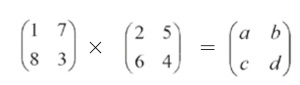
位于左上角的a是多少呢？是不是简单地把I号表左上角的1乘以Ⅱ号表左上角的2，1×2＝2就行了呢？我们要时时牢记车费表的现实意义：左上角代表了从深圳出发，还在深圳下车的总车费。1×2的确符合要求：先乘I号线在深圳游玩一阵，随后原地下车再搭Ⅱ号线再次市内游！总的路线是：深圳→深圳→深圳。起点和终点都在深圳，坐标在左上角，没错！

但是，我们忽略了另一条路线！左上角的a要求从深圳出发，最后在深圳下车，却没有规定整个过程全都在深圳市内！实际上，很容易想象另一条路线：深圳→香港→深圳，它依然符合起点和终点都在深圳的要求。这样一来，我们必须先搭I号线去香港（收费7元），在香港转搭Ⅱ号线回深圳（收费6元），它们的乘积是7×6＝42！

a最终的数值，应该是所有可能路线的叠加（深圳→？→深圳）。在本例中，只有上述两条路线，没有第三种可能了。所以a＝1×2＋7×6＝44。

很奇妙，是不是？我们再来看右上角的b。深圳出发香港下车，同样也有两种可能的路线：深圳→深圳→香港，或者深圳→香港→香港。要么先乘I号线深圳市内游再搭Ⅱ号线到香港（1×5），要么先乘I号线到香港然后转II号线香港市内游（7×4）。所以综合来说，b＝1×5＋7×4＝33。

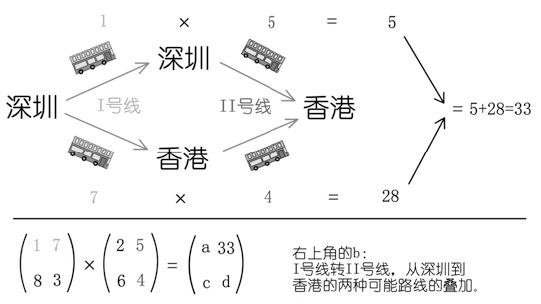
大家可以先别偷看答案，自己试着求c和d。最后应该是这样的：c＝8×2＋3×6＝34，d＝8×5＋3×4＝52。所以：

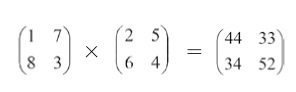
很抱歉，我们处在一个非常奇幻的世界里，虽然只是小学水平的数字运算，可能已经让有些人痛苦不堪。不过大家必须承认，我们的确学到了一些新的事物，如果你觉得这种乘法十分陌生的话，那么我们很快就要给你更大的惊奇，但首先我们还是要熟悉这种新的运算规则才是。圣人说，温故而知新，我们不必为了自己新学到的东西而沾沾自喜，还是巩固巩固我们的基础吧，让我们把上面这道题目验算一遍。哦，不要昏倒，不要昏倒，其实没有那么乏味，我们可以把乘法的次序倒一倒，现在验算一遍Ⅱ×I：

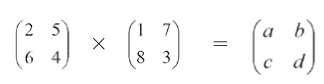
我知道大家都在唉声叹气，不过我还是坚持，复习功课是有益无害的。我们来看看a是什么，现在我们是先搭乘Ⅱ号线，然后转I号线了。我们可以先搭Ⅱ号线在深圳市内转搭I号线再次市内游（深圳→深圳→深圳），对应的是2×1。另外，还有一条路线：深圳→香港→深圳，所以是先搭Ⅱ号线去香港，在那里转搭I号线回深圳，所以是5×8＝40。所以总的来说，a＝2×1＋5×8＝42。

喂，打瞌睡的各位，快醒醒，我们遇到问题了。在我们的验算里，a＝42，不过我还记得，刚才我们的答案说a＝44。各位把笔记本往回翻几页，看看我有没有记错？嗯，虽然大家都没有抄笔记，但我还是没有记错，刚才我们的a＝1×2＋7×6＝44。看来是我算错了，我们再算一遍，这次可要打起精神了：a代表深圳上车深圳下车。所以两种可能的情况是：深圳→深圳→深圳，Ⅱ号线市内游收2块，I号线1块，所以2×1＝2。另外还有深圳→香港→深圳的路线。Ⅱ号线由深圳去香港5块，I号线由香港回深圳8块，所以5×8＝40。加在一起：2＋40＝42！

嗯，奇怪，没错啊。那么难道前面算错了？我们再算一遍，好像也没错，前面a＝2＋42＝44。那么，那么……谁错了？哈哈，难道是海森堡错了？他这次可丢脸了，他发明了一种什么样的表格乘法啊，居然导致如此荒唐的结果：I×Ⅱ ≠ Ⅱ×I。

我们不妨把结果整个算出来：

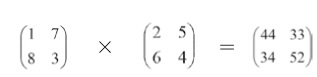
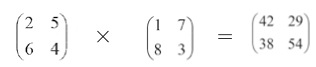
哇，真的非常不同，每个数字都不一样，I×Ⅱ ≠ Ⅱ×I！唉，这可真让人惋惜，原来我们还以为这种表格式的运算至少有点创意的，现在看来浪费了大家不少时间，只好说声抱歉。但是，慢着，海森堡还有话要说，先别为我们死去的脑细胞默哀，它们的死也许不是完全没有意义的。

大家冷静点，大家冷静点，海森堡摇晃着他那漂亮的头发说，我们必须学会面对现实。我们已经说过了，物理学，必须从唯一可以被实践的数据出发，而不是靠想象和常识习惯。我们要学会依赖于数学，而不是日常语言，因为只有数学才具有唯一的意义，才能告诉我们唯一的真实。我们必须认识到这一点：数学怎么说，我们就得接受什么。如果数学说I×Ⅱ ≠ Ⅱ×I，那么我们就得这么认为，哪怕世人用再嘲讽的口气来讥笑我们，我们也不能改变这一立场。何况，如果仔细审查这里面的意义，也并没有太大的荒谬：先搭乘I号线，再转Ⅱ号线，这和先搭乘Ⅱ号线，再转I号线，导致的结果可能是不同的，有什么问题吗？

好吧，有人讽刺地说，那么牛顿第二定律究竟是F＝ma，还是F＝am呢？

海森堡冷冷地说，牛顿力学是经典体系，我们讨论的是量子体系。永远不要对量子世界的任何奇特性质过分大惊小怪，那会让你发疯的。量子的规则，并不一定要受到乘法交换率的束缚。

他无法做更多的口舌之争了，1925年夏天，海森堡被一场热病所感染，不得不离开哥廷根，到北海的一个小岛赫尔格兰（Helgoland）去休养。但是他的大脑没有停滞，在远离喧嚣的小岛上，海森堡坚定地沿着这条奇特的表格式道路去探索物理学的未来。而且，他很快就获得了成功：事实上，只要把矩阵的规则运用到经典的动力学公式里去，把玻尔和索末菲旧的量子条件改造成新的由坚实的矩阵砖块构造起来的方程，海森堡可以自然而然地推导出量子化的原子能级和辐射频率。而且这一切都可以顺理成章从方程本身解出，不再需要像玻尔的旧模型那样，强行附加一个不自然的量子条件。海森堡的表格的确管用！数学解释一切，我们的想象是靠不住的。

虽然，这种古怪的不遵守交换率的矩阵乘法到底意味着什么，无论对于海森堡，还是当时的所有人来说，都还仍然是一个谜题，但量子力学的基本形式却已经得到了突破进展。从这时候起，量子论将以一种气势磅礴的姿态向前迈进，每一步都那样雄伟壮丽，激起滔天的巨浪和美丽的浪花。接下来的3年是梦幻般的3年，是物理史上难以想象的3年，理论物理的黄金年代，终于要放射出它最耀眼的光辉，把整个20世纪都装点得神圣起来。

海森堡后来在写给荷兰学者范德沃登（Van der Waerden）的信中回忆道，当他在那个石头小岛上的时候，有一晚忽然想到体系的总能量应该是一个常数。于是他试着用他那规则来解这个方程以求得振子能量。求解并不容易，他做了一个通宵，但求出来的结果和实验符合得非常好。于是他爬上一个山崖去看日出，同时感到自己非常幸运。

是的，曙光已经出现，太阳正从海平线上冉冉升起，万道霞光染红了海面和空中的云彩，在天地间流动着奇幻的辉光。在高高的石崖顶上，海森堡面对着壮观的日出景象，他脚下碧海潮生，一直延伸到无穷无尽的远方。是的，他知道，this is the moment（是时候了），他已经作出生命中最重要的突破，而物理学的黎明也终于到来。

饭后闲话：矩阵

我们已经看到，海森堡发明了这种奇特的表格，I×Ⅱ ≠ Ⅱ×I，连他自己都没把握确定这是个什么怪物。当他结束养病，回到哥廷根后，就把论文草稿送给老师波恩，让他评论评论。波恩看到这种表格运算大吃一惊，原来这不是什么新鲜东西，正是线性代数里学到的“矩阵”！回溯历史，这种工具早在1858年就已经由一位剑桥的数学家Arthur Cayley（阿瑟·凯莱）所发明，不过当时不叫“矩阵”而叫做“行列式”（determinant，这个字后来变成了另外一个意思，虽然还是和矩阵关系很紧密）。发明矩阵最初的目的，是简捷地来求解某些微分方程组（事实上直到今天，大学线性代数课还是主要解决这个问题）。但海森堡对此毫不知情，他实际上不知不觉地“重新发明”了矩阵的概念。波恩和他那精通矩阵运算的助教约尔当随即在严格的数学基础上发展了海森堡的理论，进一步完善了量子力学，我们很快就要谈到。

数学在某种意义上来说总是领先的。Cayley创立矩阵的时候，自然想不到它后来会在量子论的发展中起到关键作用。同样，黎曼创立黎曼几何的时候，又怎会料到他已经给爱因斯坦和他伟大的相对论提供了最好的工具。

乔治•盖莫夫写过一本极受欢迎的老科普书《从一到无穷大》（One, Two, Three…Infinity），这本书如此风靡全球，以致最近还出了一个新的中文版。盖莫夫在书里说，目前数学只有一个大分支还没有派上用场（除了做做智力体操之外），那就是数论。不过盖莫夫说这话时却没有想到，随着计算机革命的到来，古老的数论已经以惊人的速度在现代社会中找到了它的位置，开始大显身手。基于大素数原理的加密、解密和数字签名算法（如著名的公钥算法RSA）已经成为电子安全不可缺少的部分。我们每天上网和进行电子交易的时候，全靠它们的保护才使得黑客无法顺利地窃听你的隐私信息。我们在史话后面谈到量子计算机的时候还会回到这个话题中来。

到今天为止，数论领域里已经有许多著名的难题被解开，比如四色问题，费马大定理。也有比如哥德巴赫猜想，至今悬而未决。天知道，这些理论和思路是不是也会在将来给某个物理或者化学理论开道，打造出一片全新的天地来。