针对人们对MWI普遍存在的误解，近来一些科学家也试图为其正名，澄清宇宙本身实际并未在物理上真的“分裂”，而只是一个比喻而已，这并非MWI和埃弗莱特的本意[如Tegmark1998。]，我们在这里也不妨稍微讲一讲。当然我们的史话以史为本，在理论上尽量试图表达得浅显通俗，所以用到的比喻可能不太准确。真正准确地描述这个理论要用到非常复杂的数学工具和数学表达，希望各位看官对此心中有数。

首先我们要谈谈所谓“相空间”的概念。读过中学数学的人都应该知道，2维平面中的一个点可以用含有两个数字的坐标来表达它的位置，而3维空间中的点就需要3个数字。我们现在需要扩展一下思维：假如有一个4维空间中的点，我们又应该如何去描述它呢？显然，我们要使用含有4个变量的坐标，比如（1,2,3,4）。如果我们用的是直角坐标系，那么这4个数字便代表该点在4个互相垂直的维度方向的投影，推广到n维空间，也是一样。诸位大可不必费神在脑海中努力想象4维空间是个什么样的东西，这只是我们在数学上的构造而已，关键是我们必须清楚：n维空间中的一个点可以用n个变量来唯一描述，而反过来，n个变量也可以用一个n维空间中的点来涵盖。

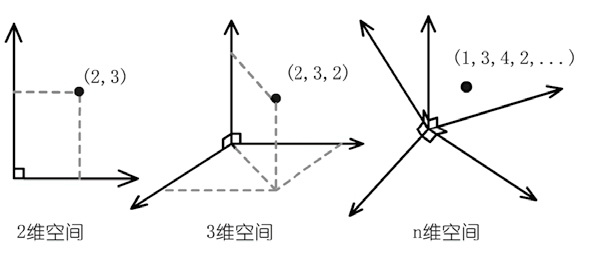
现在让我们回到物理世界，我们如何去描述一个普通的粒子呢？在每一个时刻t，它应该具有一个确定的位置坐标（q1, q2, q3），还具有一个确定的动量p。动量是一个矢量，在每个维度方向都有分量，所以要描述动量p还得用3个数字：p1，p2和p3，分别表示它在3个方向上的速度。总而言之，要完全描述一个物理质点在t时刻的状态，我们一共要用到6个变量，而我们在前面已经看到了，这6个变量可以用6维空间中的一个点来概括。所以，用6维空间中的一个点，我们可以描述1个普通物理粒子的经典行为。我们这个存心构造出来的高维空间就是系统的相空间。

假如一个系统由2个粒子组成，那么在每个时刻t这个系统则必须由12个变量来描述了。但同样，我们可以用12维空间中的一个点来代替它。对于一些宏观物体，比如一只猫，它所包含的粒子可就太多了，假设有n个吧，不过这不是一个本质问题，我们仍然可以用一个6n维相空间中的质点来描述它。这样一来，一只猫在任意一段时期内的活动其实都可以等价为6n维空间中一个点的运动（假定组成猫的粒子数目不变）。我们这样做并不是吃饱了饭太闲的缘故，而是因为在数学上，描述一个点的运动，哪怕是6n维空间中的一个点，也要比描述普通空间中的一只猫来得方便。在经典物理中，对于这样一个代表了整个系统的相空间中的点，我们可以用所谓的哈密顿方程去描述，并得出许多有益的结论。

在我们史话的前面已经提到过，无论是海森堡的矩阵力学还是薛定谔的波动力学，都是从哈密顿的方程改造而来，所以它们后来被证明互相等价也是不足为奇。现在，在量子理论中，我们也可以使用与相空间类似的手法来描述一个系统的状态，只不过把经典的相空间改造成复的希尔伯特矢量空间罢了。具体的细节读者们可以不用理会，只要把握其中的精髓：一个复杂系统的状态可以看成某种高维空间中的一个点或者一个矢量。比如一只活猫，它就对应于某个希尔伯特空间中的一个态矢量，如果采用狄拉克引入的符号，我们可以把它用一个带尖角的括号来表示，写成：|活猫>。死猫可以类似地写成：|死猫>。

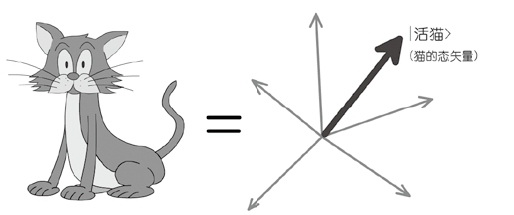
说了那么多，这和量子论或者MWI有什么关系呢？

让我们回头来看一个量子过程，比如那个经典的双缝困境吧。正如我们已经反复提到的那样，如果我们不去观测电子究竟通过了哪条缝，则其必定同时通过了两条狭缝。也就是说，它的波函数|ψ＞可以表示为：

只要我们不观测，它便永远按薛定谔波动方程严格地发展。为了表述方便，我们按照彭罗斯的话，把这称为“U过程”，它是一个确定、经典、可逆（时间对称）的过程。值得一提的是，薛定谔方程本身是线性的，也就是说，只要|左＞和|右>都是可能的解，则a｜左> + b｜右>也必定满足方程！不管U过程如何发展，系统始终会保持在线性叠加的状态。

但当我们去观测电子的实际行为时，电子就被迫表现为一个粒子，选择某一条狭缝穿过。拿哥本哈根派的话来说，电子的波函数“坍缩”了，最终只剩下|左>或者|右>中的一个态独领风骚。这个过程像是一个奇迹，它完全按照概率随机地发生，也不再可逆，正如你不能让实际已经发生的事情回到许多概率的不确定叠加中去。还是按照彭罗斯的称呼，我们把这叫做“R过程”，其实就是所谓的坍缩。如何解释R过程的发生，这就是困扰我们的难题。哥本哈根派认为“观测者”引发了这一过程，个别极端的则扯上“意识”，那么，MWI又有何高见呢？

它的说法可能让你大吃一惊：根本就没有所谓的“坍缩”，R过程实际上从未发生过！从开天辟地以来，在任何时刻，任何孤立系统的波函数都严格地按照薛定谔方程以U过程演化！如果系统处在叠加态，它必定永远按照叠加态演化！

可是，等等，这样说固然意气风发，畅快淋漓，但它没有解答我们的基本困惑啊！如果叠加态是不可避免的，为什么我们在现实中从未观察到同时穿过双缝的电子，或者又死又活的猫呢？

让我们来小心地看看埃弗莱特的假定：“任何孤立系统都必须严格地按照薛定谔方程演化”。所谓孤立系统指的是与外界完全隔绝的系统，既没有能量也没有物质交流，这是个理想状态，在现实中很难做到，所以几乎是不可能的。只有一样东西例外——我们的宇宙本身！因为宇宙本身包含了一切，所以也就无所谓“外界”，把宇宙定义为一个孤立系统似乎是没有什么大问题的。宇宙包含了n个粒子，n即便不是无穷，也是非常非常大的，但这不是本质问题，我们仍然可以把整个宇宙的状态用一个态矢量来表示，描述宇宙波函数的演化。

MWI的关键在于：虽然宇宙只有一个波函数，但这个极为复杂的波函数却包含了许许多多互不干涉的“子世界”。宇宙的整体态矢量实际上是许许多多子矢量的叠加和，每一个子矢量都是在某个“子世界”中的投影，分别代表了薛定谔方程一个可能的解！

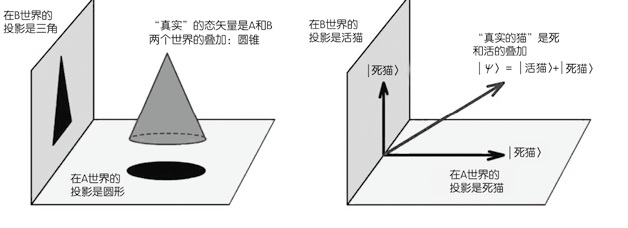
为了各位容易理解，我们假想一种没有维度的“质点人”，它本身是一个小点，而且只能在一个维度上做直线运动。这样一来，它所生活的整个“世界”，便是一条特定的直线。对于这个质点人来说，它只能“感觉”到这条直线上的东西，而对别的一无所知。现在我们回到最简单的二维平面：假设有一个矢量（1,2），我们容易看出它在x轴上投影为1，y轴上投影为2。如果有两个“质点人”A和B，A生活在x轴上，B生活在y轴上，那么对于A君来说，他对我们的矢量的所有“感觉”就是其在x轴上的那段长度为1的投影，而B君则感觉到其在y轴上的长度为2的投影。因为A和B生活在不同的两个“世界”里，所以他们的感觉是不一样的！但事实上，“真实的”矢量只有一个，它是A和B所感觉到的“叠加”！

我们的宇宙也是如此。“真实的，完全的”宇宙态矢量存在于一个非常高维（可能是无限维）的希尔伯特空间中，但这个高维的空间却由许许多多低维的“世界”所构成（正如我们的三维空间可以看成由许多二维平面构成一样），每个“世界”都只能感受到那个“真实”的矢量在其中的投影。因此在每个“世界”感觉到的宇宙都是不同的。

总之，按照MWI，事情是这样的：“宇宙”（Universe）始终只有一个，它的状态可以为一个总体波函数所表示，这个波函数严格而连续地按照薛定谔方程演化。但从某一个特定“世界”（World）的角度来看，则未必如此。波函数随着时间的流逝变得愈加复杂，投影的世界也越来越多，薛定谔方程的每一个可能的解都一定对应了一种投影，因此一切可能发生的事情都在某个“世界”发生了。为了简便起见，在史话后面的部分里我们还是会使用“分裂”之类的词语，不过大家要把握它的真正意思。也有另一种叫法，把每一个投影的分支都称为“宇宙”（Universe），而把总体的波函数称为“多宙”（Multiverse）[比如下面我们即将遇到的多宇宙派物理学家David Deutsch。]，这只是用词上的不同，包含的其实是一个意思。“多宇宙”和“多世界”，指的是同一个理论。

然而，还剩下一个问题：好吧，假如说电子每次通过屏幕的时候都不曾“坍缩”，只不过两个世界的我们观测（或感觉）到不同的投影罢了，但为什么我们感觉不到别的世界呢（就比如说观测到活猫就无法同时观测到死猫）？而相当稀奇的是，未经观测的电子却似乎有特异功能，可以感觉来自“别的世界”的信息。比如不受观测的电子必定同时感受到了“左缝世界”和“右缝世界”的信息，不然如何产生干涉呢？这其实还是老问题：为什么我们在宏观世界中从来没有观测到量子尺度上的叠加状态呢？

在埃弗莱特最初提出MWI的时候，这仍然是一个难以解释的谜题。不过进入70年代以后，泽（Dieter Zeh）、苏雷克（Wojciech H Zurek）、盖尔曼（Murray Gell-Mann）等科学家提出了一种极其巧妙的理论。它迅速发展并走红，至今已经得到了大部分人的支持，这就是所谓的退相干理论（decoherence theory）。