相变是“日常物理”的现象，我们对此习以为常，也不当回事。但是对于物理学家来说，这些非常有趣的现象都是值得研究的。这就是为什么在20世纪70年代初，我也投入了一些精力研究某些类型的相变，直到1971年和1972年，这些相变仍然是一个悬而未决的问题。

众所周知，在100℃的温度下，水开始沸腾，也就是说，它从液相进入气相，同理，在0℃时，它从液相进入固相，也就是冰。

对物理学家而言，观察这些“正常”现象的同时可以提出无数问题：为什么会发生这样的转变？为什么要在这么精确的温度下？所有材料都会出现类似的现象吗？当然还有一些问题，现在很难找到答案。

在20世纪的第一个十年，物理学家开始用实验证据证明原子和分子作为构成物质的“砖块”而存在，因此也试图解释一些宏观现象，比如水结成冰，认为都是由这些极小物质单位的集体行为导致的。

从微观角度来看，相变变得越来越难以描述，而且代表着一个总以不同形式呈现的周而复始的问题。于是，我们从解决最简单的案例入手，一点一点改进我们的工具，把问题一个一个解决。

为了在微观层面研究相变，我们需要了解许多“物质”的行为，比如原子、分子或小磁针，“基本物体”如此之多，我们可以利用比传统物理学更广泛的语境，将它们称为“单元”，它们之间相互作用，彼此交换信息，并根据接收到的信息改变自己的行为。

就物理学而言，“交换信息”相当于“受力”，但一般来说——由于模型可以应用于许多研究领域，从物理学到生物学，再到经济学等等——我们有很多个体，它们的行为取决于与之或远或近的其他个体的行为，通常距离都非常近，因为距离太远的个体之间是无法交换信息的。

我们能够在宏观层面测量的物理量，例如水温，取决于微观单元的行为，比如我们无法观察到的分子的运动速度。

想象一下，用灵敏度非常高的显微镜观察水。我们会看到微微弯曲的哑铃状分子在不断移动、相互吸引、旋转、彼此远离和快速振动。这是在分子水平上对水的描述。然而用肉眼观察水的时候，我们看到的是一种液体，在一定温度下结冰，变成固体，在另一温度下蒸发，变成气体。如何从单个原子的行为转移到系统的整体行为，是一个需要花时间进行解释的问题。

一级相变

某种状态变化会在什么温度和压力下发生，研究相变的人对此不大感兴趣，他们的兴趣点在于发现其中的机制。例如，为什么这一现象会突然发生，而且发生在一个特定的“点”上？在100℃时，系统发生了哪些变化？为什么在只低于临界温度1℃的情况下观察这个系统时，我们就什么也看不到呢？为什么再高1℃就足以让宏观行为发生骤变？

从概念上讲，解决这个问题绝非易事，以至于20世纪30年代许多物理学家想弄清楚，物理学的一般规律，特别是统计力学的一般规律，是否可以用来解释相变问题。

这个问题在20世纪四五十年代得到解决，甚至是从物理学中一个相当普遍的概念出发的，即能量最小化。在自然界中，一个自由移动的物体会试图达到其能量最小的位置，直到找到平衡点。例如，滚下来的球会滚到坑底。坑底代表了稳定的平衡位置，除非有什么外力介入，否则球不会离开那里。

冰也有类似的情况，它在低于0℃时，处于稳定平衡状态（固相），对应着它的最小自由能。随着温度升高，在固相中占据晶格确切位置的分子开始振荡，直到失去固定位置并自由运动。这就是液相，同样代表稳定平衡状态，对应着另一个自由能的最低点。

给水提供热量就像推动一个球，即便推力很小，球也会开始移动，只不过没有足够的能量让它从坑里出来。推力变大时，球将获得足够的能量离开坑底，一直移动，直至找到另一个平衡位置。

因此，当温度升高，停留在固相晶格中的水分子将会更剧烈地振荡，直到0℃时，把它们连接在一起的键会开始断裂。在这一阶段继续提供热能，温度不会再升高了，但系统获得的能量会使分子之间的键断裂，直到冰全都融化成水，并在液相中找到新的稳定平衡态。

这种相变被称为一级相变，其特点是两个重要的现象。

第一个现象是该系统在接近临界点时，没有任何微观特征表明它即将发生转变。温度为0.5℃的水没有结冰的迹象，但当温度再降低半度，水就开始结冰了。系统在临界温度附近时，既不会形成水中的冰凌，也不会有冰中的积水。

第二个重要的现象是潜热的存在，即破坏分子键而不提高系统温度所需的热能。当冰处于0℃时，我们提供的热能会破坏分子键，直到所有的冰融化。我们必须给系统提供使其改变状态的热能，准确地说就是潜热。

有时我们可以把这些相变描述为系统从有序到无序的转变。事实上，在固相中，水分子占据晶格中的确切位置，因此处于有序相。在液相中，水分子可以自由移动，所以其微观情况就显得比此前的固相无序得多。

二级相变

并非所有材料都表现得像水一样。还有一些相变是在没有潜热的情况下发生的，也就是说不必提供一定的热能，一旦达到临界温度就可以从一个相转入另一个相。

在这种情况下，随着临界温度逐渐接近，相变连续发生，可以说是平缓地发生。这种变化被称为二级相变。

我们举个例子：磁铁在常温下是一个磁性系统，随着温度升高，磁性会消失。用术语来说，就是磁铁从铁磁相（磁性）转变为顺磁相（非磁性）。

让我们看看系统内部究竟发生了什么。可以将磁铁的磁场想象成空间中有指向性的箭头，就像指南针的指针一样，箭头的尖都指向北。

这个宏观的磁场由系统中单个粒子的基本磁场的总和形成，这些基本磁场被称作自旋。在磁铁内部，自旋之间存在的相互作用使它们整齐地朝向同一边，也就是说大量的小箭头都指着同一方向。

即使在磁化的情况下，相变也会随着温度的升高而发生。事实上，提供给磁铁的热能会导致自旋的运动增加，从而改变它们的方向。因此，它们将倾向于混乱，最终失去秩序。正是自旋有序的排列才产生了宏观的磁场，随着温度升高，磁场将会减弱，直到完全消失。

在这种情况下，我们也可以将相变描述为系统在有序相和无序相之间的变化。

为了帮助理解，我们可以使用1924年还是学生的恩斯特·伊辛在博士论文中提出的模型，这可能是物理学家发明的第一个以极简的描述来帮助理解真相的模型。如图1所示，该模型只允许自旋有两个方向——向上或向下，其他方向都被禁止。

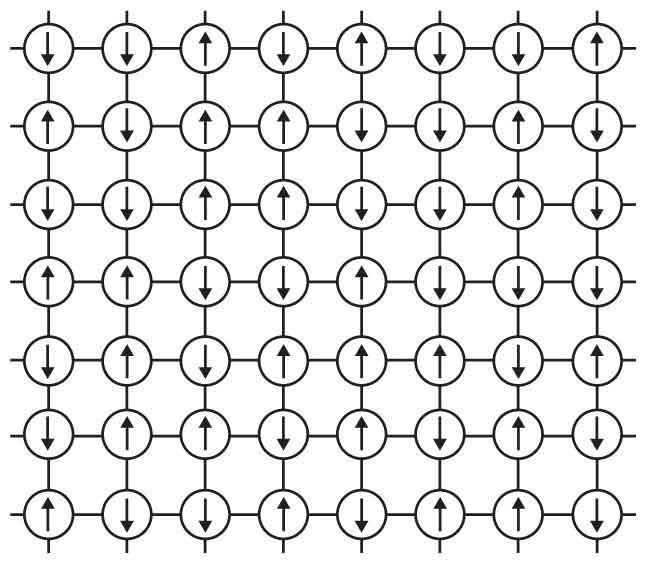
自旋之间存在的力使得它们倾向于在方向上保持一致（全部向上或全部向下），而热扰动会倾向于使它们站不齐队，并让其中一些的方向倒置过来，与别的相反。

铁磁相意味着大多数自旋方向相同（有序相），顺磁相则意味着会有50%的自旋指向上，剩下的50%指向下，完全随机分布（无序相）。

我们也可以用对称性来描述这个系统。如果一个变换不会改变系统的性质，我们可以说它是系统的对称性。

我们以“所有自旋的翻转”变换为例。如果这个变换出现在无序相或顺磁相，则什么都不会改变，我们总是有50%的自旋向上，50%的自旋向下，而且总是随机分布，这就是系统的对称性。

然而，在临界温度以下，大多数自旋指向同一个方向时（如图2a所示，其中大多数小圆点为灰色），它们的翻转会导致原来的宏观磁场发生翻转，从而改变标记的颜色（也就是大多数小圆点将变为白色）。所以对于有序相或铁磁相而言，自旋的翻转不是一成不变的，因为它让磁场翻转了。

在这种情况下，我们就会说两个相之间出现了“自发对称性破缺”：原本存在于顺磁相中的对称性（自旋翻转），相变后系统转为铁磁相时就不再存在了。在没有外部现象参与的情况下，原来的对称性自发地打破了。

铁磁相变属于二级相变类别中的一类，其特征可以概括为一个参数，在这种情况下参数是磁化强度，被称为“序参量”，表示系统在有序相和无序相之间转变的过程。

乍看上去，磁性系统似乎比我们此前见过的水这一类系统更简单，因为两个相之间没有间断。但麻烦都出在细节上，二级相变的情况中，细节极其错综复杂。

我们拿一块保持在高温下的磁铁，这样它就不会产生任何磁化，然后把它放在磁场中，慢慢降低它的温度，当接近临界温度时，我们会看到系统越来越容易磁化。一旦达到临界温度，相变就会发生，磁铁自身产生磁化，而不需要外部磁场。

在磁铁内部，会产生越来越大的铁磁岛[在铁磁岛内部，磁场方向相同。]。两个相共存的情况（如图3所示）研究起来非常复杂。

普适类

实验物理学家发现了一个有趣的事实：在很大程度上，磁性系统的行为并不取决于形成它的基本单元的行为。

虽然磁性物质千差万别，各种微观成分之间的相互作用和对量子细节的描述也各不相同，但我们可以看到，磁化强度在接近临界温度时会如出一辙地趋于零。这一趋势在数学上可以用一个幂律函数表示，该函数的指数有相同的数值，我们称之为β指数，所有类型的磁性物质都适用，尽管这些物质彼此有很大不同。

这就好像一级方程式赛车在比赛中各显神通，但到了最后一圈，大家都不约而同地减慢速度，以便能停在终点线上。

这是一个出乎意料的非凡发现：虽然微观细节完全不同，但集体行为却是相同的。利奥·卡达诺夫将这一结果形式化，提出了将相变现象划分为多个普适类的概念。其β指数具有相同值的现象属于同一类别。

这不禁使人想起柏拉图的自然观。我们可以说，临界行为的普适类数量相对较少，每个真实系统都可以归入某个普适类（用柏拉图的术语来说，也就是归入一种理念）。

类别的划分取决于系统基本成分的自由度。比如说，各种自旋的自由度是不同的，这要看它是可以在三维空间中运动，还是被约束在平面上运动，或者只能自己旋转。总之，这取决于我们要研究的物质的基本成分能在多大程度上和以何种方式进行运动，β指数的值只取决于这些自由度。

20世纪70年代初，这个问题——我们很快就会看到一个具体的例子——才真正引起人们的兴趣，大家的感觉是，只要找到恰当的形式体系来计算临界指数，就会有各种各样的工具来解决这个问题。所以，我开始研究相变，认为在很短的时间内就会找到答案，然后再回过头来研究基本粒子的未解之谜，这似乎才更具挑战性。

尺度不变性

实质上，这项研究是关于自旋之间有较强磁性相互作用的系统的。那时人们已经在微观层面上认识到了这些相互作用，因此必须找到一套形式体系，从已知的微观描述出发，旨在从中间层面描述系统，而不再涉及微观细节，因为磁化行为并不取决于这些细节。借助这个中间层面，即所谓介观层面，我们研究系统的涨落，也就是研究大量原子如何从一个相过渡到另一个相。

通过研究这些涨落及其相互作用，可以分析系统的演化过程。这些涨落与用来分析系统的尺度无关，我们很快就会谈到这一点。

这项工作已经取得了很大的进展，比如乔瓦尼·约纳-拉西尼奥和卡洛·迪·卡斯特罗二人，他们详细研究了介观行为的起源。肯尼斯·威尔逊则向前迈出了非常重要的两步，他在1971年和1972年发表的一些文章中，介绍了如何建立一套能够计算临界指数的理论。这种被称作“重整化群”的理论，为他赢得了1982年的诺贝尔物理学奖。

重整化群

要想理解为什么威尔逊提出的处理二级相变的技术被称为“重整化群”，就需要对他使用的方法有大致的了解。

在介观层面对系统进行描述，意味着尺度改变但描述不变，也就是说，我们观察的结果不取决于我们使用多大的变焦镜头。

我们看图4。

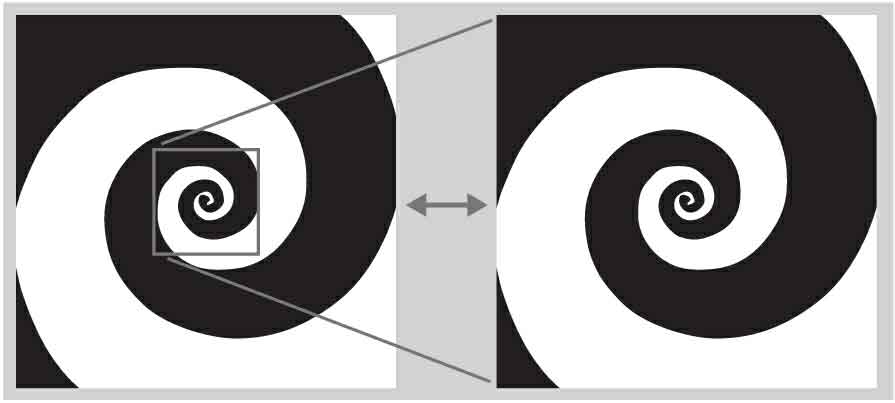
右图是左图正方形的局部放大。如图所示，无法通过改变观察尺度或者观测时的焦距来区分这一系统。

让我们回到图3所示的系统。除了尺度的因素以外，它们的涨落行为基本上是相同的，越是“从远处”（我们可以考虑使用广角镜头）观察系统，涨落就越小，越接近（调整焦距），看到的涨落就越大。

卡达诺夫已经提出了这个想法，就是将系统划分为包含一定数量自旋的方格。我们来看图5a：每个3×3的方格有9个自旋。下一步是计算这9个自旋中有多少向上（黑色方格）、多少向下（白色方格）。取左上角3×3的方格为例，我们看到它包含6个黑色方格和3个白色方格，所以黑色的占大多数。我们将这个刚刚得出的值用在右图（图5b）中，将其视为一个单一的整体，即一个单独的自旋。图5b左上角的方格实际上是黑色的。组成图5b的每个方格都是一个自旋，这个自旋的颜色由初始区域的9个自旋中大多数方格的颜色决定。

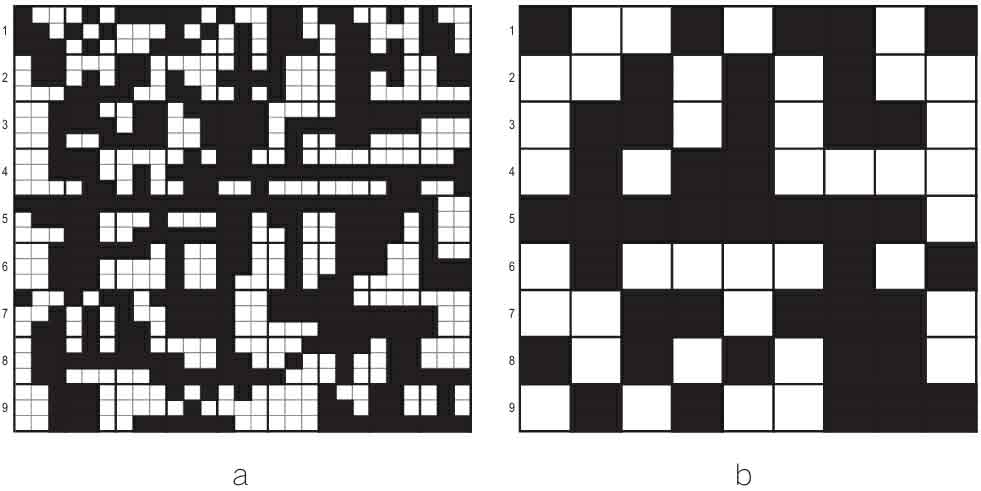
简言之，我们使用了一种类似于美国总统选举的机制：总统候选人如果在一个州赢得多数票，就可以获得该州所有的选举人票数。

每次我们这样操作时，实际上都是在改变尺度，并大大减少要考虑的变量数量（不必考虑图5a左上角最开始的那9个自旋，现在图5b的第一个方格中只有1个自旋而已）。

以这种新方式来描述我们的系统（在更大的尺度上）也不失为一种好方法，其实我们只是通过“更大的颗粒”来观察它罢了。威尔逊的技术让这项研究从一个尺度转入下一个尺度，因此被称为“重整化”。

就这样，在20世纪70年代初，磁性系统的相变得到了恰当的描述，于是我又回到了基本粒子物理学的研究道路上。