互联网日常应用中涉及的大部分人工智能都基于自旋玻璃和神经网络的理论。

一生中最有价值的研究成果之所以能够问世，可能是因为你在去别处的路上与之不期而遇。

我就是这样。人们认为我对物理学最大的贡献就是提出了自旋玻璃理论，这是我在研究基本粒子问题时应运而生的。

那时候，为了解决这个问题，最合适的工具似乎是一种数学技术，名为复本法，而我当时还没有掌握。我搜集了关于这个问题的所有文献，开始进行研究。所谓的复本法，是一种数学方法，即取一个系统，进行多次复制，然后比较多个复本的行为表现。这种方法看上去完全能够解决我研究的问题，但是在一份文献描述的案例中，以它得出的结果完全离谱，让人不知所云。

面对一个新问题，当我还没有明确的认识时，选择一种可能不奏效的工具并非明智之举。这就像在使用指南针的时候，它时常指向南方，而不是北方，但谁也不知道它什么时候指南，什么时候指北，也不知其原因。

所以我决定先弄清楚这个工具到底可不可靠。

那是1978年圣诞节前夕，当时我在弗拉斯卡蒂实验室工作。我复印了一篇文章，论述的是复本技术导致不可靠结果的案例。假期里我一直把这篇文章带在身边。

文章讨论了关于无序系统和自旋玻璃的问题，这些问题与我当时的研究领域相去甚远，我也从未涉猎过。然而对于理解这种方法为何在研究中不起作用，这篇文章又至关重要。我研究了文章用的模型，又验算了所有的数据，这些都是对的，但结果却不合逻辑。这个问题就值得深究了。

度假回来后，我做了一些进展非常顺利的工作，答案似乎唾手可得。我试图以一些更加先进的研究成果为起点来解决这个问题，认为这样会轻而易举，但越是努力，问题就越难解决。

如果有些结果一致，有些结果又与数值模拟的值相去甚远，这就意味着研究结果还差得很远。或许有必要彻底改变看问题的角度。

不知不觉中，我已经开始探索一个新的研究领域。我不再思考初心所指的基本粒子问题，我的兴趣被别的东西激发了。

自旋玻璃

自旋玻璃指的是一种金属合金，取这个名字是因为它们的磁性相变，这一相变是由形成合金的粒子的自旋行为所致，其表现类似于玻璃的相变。

这些合金由贵金属形成，比如金、银，其中含有少量被稀释的铁。在高温下，它们的行为类似于一般的磁性系统，但当温度下降到某个值以下时，就会出现类似于玻璃、蜡或沥青的行为：变化越来越慢，系统似乎永远不会达到平衡状态。

在学校里我们都学过，液体是一种被注入固体容器后就会呈现容器形状的材料。玻璃在高温下显然是液体，但很明显，这种液体表现出不寻常的行为。例如，如果我们把一个装满熔融玻璃（或蜂蜜、蜡）的容器倒过来，液体不会立即倒在地板上，而是开始慢慢地从容器中“滴落”。玻璃越是冷却，滴得就越慢，由于某种原因，这一系统行为的速度大大减慢。

当温度下降时，系统动力学中的急剧变慢与金属合金的磁化行为有一些相似之处。这就好比在降低温度时，自旋翻转的可能性同时降低，因此不可能达到平衡状态。

让我们回到前面第一章中的例子，想象一辆满载乘客的公共汽车，只要密度相对较低，想从一个点到另一个点的人就可以让其他人避让而自己顺利通过。当然，那些避让的人也会再使别人挪动位置，产生连锁反应。只要有足够的空间，一切都可以正常进行。但是，密度越高，接触越紧密，人与人之间的空间越小，移动起来就越困难，越容易被卡住。英国人称之为“traffic jam”（“拥堵”或“交通堵塞”）。

这种现象相当普遍（涉及玻璃、蜡、蜂蜜、沥青、金属合金……），促使学者们纷纷研究其原理。解决这个问题最好的办法是建立一个起步简单的模型，重现这种现象。这一过程有可能让我们发现温度变化时导致动力学变慢的基本特征或相互作用。这些特征和相互作用存在于玻璃、蜂蜜、蜡、沥青和某些金属合金中，但在水或其他大多数液体中应当不存在。

模型

从实验的角度来看，研究这些材料的相变也相当困难。我可以告诉你们一件有意思的事，在澳大利亚，一项独一无二的实验正在进行。科学家们采集了一定量的沥青，在控制温度的情况下，沥青仍然保持一定的黏度（因此沥青不完全静止并能形成液滴），他们要测量这些沥青滴落的频率。该实验始于1927年，到2014年为止只滴落了9滴。后来我就不再关注这个实验了，很难想象再过多久我们才会看到一些有趣的结果……

这些系统研究起来很复杂，最好的办法当然是建立一个比实际情况简单的综合模型，这可以帮助我们找到答案。

为了理解什么是模型，以及它对理论物理学家的用处，我们可以把它想成大富翁游戏。这是一种社会模型，只包含几条简单的游戏规则，包括土地的支配权和费用、建筑费用和房地产租金的数额。再加上我们生活中经常遇到的偶然因素，通过掷骰子的方式移动，让“意外”和“概率”来决定玩家是走出困境还是陷入僵局。

有了这些简单的规则，只要玩上一会儿，你们就会意识到资本主义制度的一个特征：有钱人会变得越来越富有。

虽然大富翁游戏不能涵盖现实社会的所有复杂性，但却能够从中把握某些特征。同样道理，物理学家建立的模型也不能包含真实系统的所有复杂性，但如果我们能为模型有意制定一些规则，就有希望看到模型成功重现研究现象的一些基本特征。

一旦建立了模型并制定了描述其运行的规则，就可以让系统进行演化，也就是说，可以开始我们的大富翁游戏了，或者说我们就可以通过升高或降低这个综合模型中定义的温度，用计算机模拟系统的相变。

这个不断演化的模型将会产生一些结果，就像玩大富翁的时候“有钱人会变得越来越富有”一样，或者像伊辛模型显示的那样，铁磁相变会在温度降低时出现。

这样，我们就可以开始着手发展我们的理论，即从综合模型的规则和初始数据出发，建立可以重现模拟结果的数学结构。这种实验室不再由磁铁、电路、电炉或其他传统实验设备组成，现在它用的是计算机，我们用计算机重现的并非金属合金的变化，而是模型的运转。

如果成功做到了这一点，接下来就要弄清，我们建立的这个理论是否真的可以在实际情况中应用，从而解决金属合金、玻璃、蜡和其他许许多多系统的问题。

自旋玻璃模型

在此前看到的伊辛模型中，自旋之间的力是这样的：在低温下，它们倾向于朝同一方向看齐，要么全部向上，要么全部向下。

然而，在自旋玻璃模型中，作用于某些自旋对之间的力则倾向于使自旋朝向相反的方向，这就使情况变得复杂了。

让我们来举个实际的例子。在生活中，我们往往很容易意识到自己的目标与别人的不一致，因此不得不放弃自己的追求。例如，我想与甲先生和乙先生成为朋友，但不幸的是，他们二人不睦，因此我很难同时与他们成为非常要好的朋友。这种情况本身令人沮丧不已，但涉及很多人时，就会变得更加复杂。

我们想象一部这样的悲剧：两个群体之间有一场争斗，剧中的每个角色都必须选边站队。而且，他们每个人对别人都有强烈好恶（这真是一出悲剧！）。简单起见，我们可以假设他们之间喜欢与厌恶的感觉都是相互的（今天已经开发出了一些方法，可以处理他们之间感觉并非相互的情况）。

我们从这部剧中选取三个角色，安娜、雅丽和保罗。如果这三个人彼此都很友善，那就没有问题了，他们会选择同一队。同样简单的结果是，如果他们中的两个人关系很好，并且都讨厌第三个人，第三个人也讨厌他们，在这种情况下，志趣相投的两个人会选择同一队，而剩下那个人将选择另一队。但是，如果他们三人互相看不顺眼，又会有怎样的结果呢？这会造成一定程度的沮丧感，因为有两个互不喜欢的人必然会在同一队中。

当许多这样的三人组感到沮丧时，情况显然就开始变得不稳定了，有些人可能会换到另一队，试图找到总体沮丧程度相对较低的状态。我们可以将这种“戏剧张力”定义为沮丧三人组的数量除以所有三人组的总数。

详细的研究表明，在莎士比亚的悲剧中，这样定义的戏剧张力在悲剧开始的时候非常小，剧情进行到一半的时候达到峰值，最后在悲剧结束时减小。

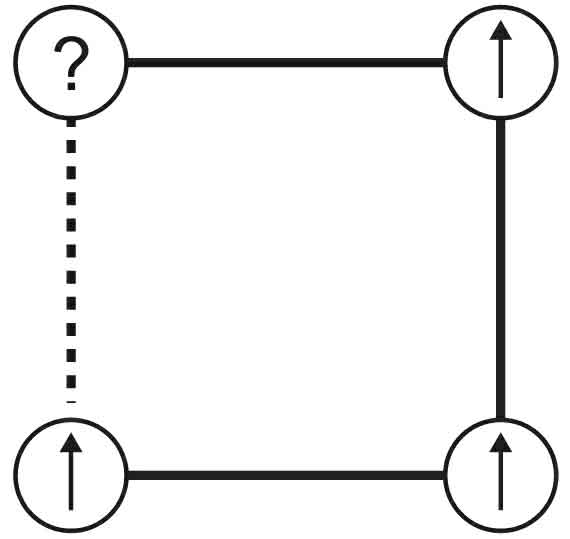
在图6的自旋玻璃示意图中，不再有三元组，而是将自旋置于方形网格上，每个自旋只能向上或向下（禁止朝向其他方向）。刚才说的“友善关系”，现在我们称之为“铁磁键”，这是倾向于让自旋指向同一方向的力，在图6中我们用实线表示。而前面讲的“厌恶关系”就变成了“反铁磁键”，用虚线表示，这代表倾向于让自旋指向相反方向的力。同样，我们可以很容易地验证它们是否存在阻挫（“沮丧感”）。来看看图7的例子。

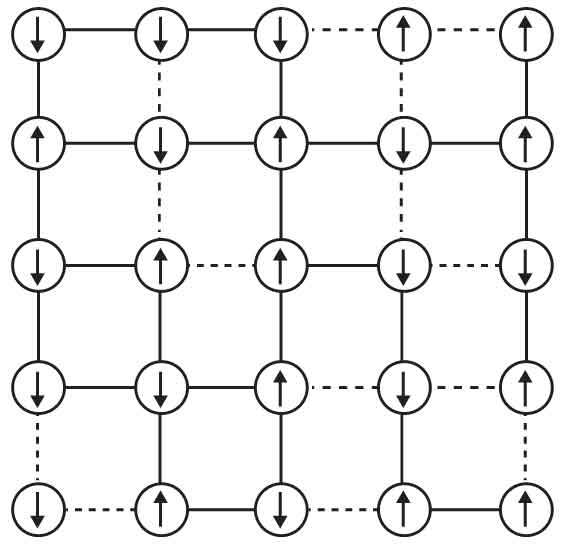
在这种情况下，左上角的自旋与其下方的自旋之间有一个反铁磁键，但与右侧的自旋之间有一个铁磁键，这样的话它只能满足这两个键中的一个，所以并不知道它会向上还是向下。

最早的自旋玻璃模型是由爱德华兹和安德森提出的，但更简单的模型是谢林顿和柯克帕特里克在1975年建立的。

现在回到我的问题上来，如果使用复本法来计算谢林顿和柯克帕特里克模型描述的自旋玻璃系统的物理量，会遇到一系列不合逻辑的问题。例如，计算得到的熵会出现负值，这是不可能的，因为在每个物理系统中，熵都是一个被定义为正值的变量。如果一个系统中熵的计算结果是负值，要么计算结果是错的（这种情况有可能发生，但事实并非如此，因为我们都进行了检查），要么某个地方存在概念性错误。

寻求解决办法

我最初犯的概念性错误有两个。第一个是技术上的错误，很难向非专业研究人士解释清楚，总之是与错误的数学假设有关。

另一个是物理上的错误，因为我不知道我正在研究的现象有哪些特征（后来我花了三年多的时间才弄明白我所做的这个数学解的物理意义）。

1979年，在我写的第一篇关于这个内容的文章中，我明确指出，可以使用一个给定的结构来部分解决这一问题。文章最后，我兴奋地补充道：“这个结构可以推广，以便得到完备的解决方案。”

正如科学论文通常的遭遇，我这篇文章在发表之前被送到了一位评审专家那里，也就是一位能看懂文章并决定是否值得发表的同行。他的评语大致是说：“帕里西做的东西让人完全不能理解。然而，由于方程给出的结论符合数值模拟的结果，因此这篇文章也可以发表。至于文中提到推广此方法以适用于更复杂情况的部分，不必赘述。”后来这篇文章发表了，不过我删去了最后一部分内容。

抛开这些轶事不谈，其实那时候我真的不知道自己在做什么。我已经找到了一些处理问题的规则，并加以应用，最后经过一系列的步骤建立了方程，而且是有意义的，最重要的是，通过方程得到的结果与数值模拟的数据完全相符，还得到了熵的正值。

但在“计算过程”中发生了什么我还没弄明白，这就像进入一条隧道，然后却发现自己莫名其妙地从另一头出来了。

在接下来的一篇文章中，理论结果和模拟结果之间的一致性表明，我的理论是有意义的，但这种意义仍然不够清晰。

我没弄懂的物理问题与物理学家所谓的序参量有关。正如我们所看到的，系统中的状态转换通常以参数的变化为特征。例如，研究液体和气体之间相变的序参量是密度。在铁磁相变中，要研究的序参量是磁化强度。在相变过程中，序参量会发生变化，例如密度或磁化强度，其不同数值的物理意义是很容易理解的。

然而令人感到意外的是，在我对自旋玻璃的计算结果中，序参量不再是一个在相变过程中值会发生变化的简单数字：在相变过程中变化的居然是一个函数。一个值是不足以描述相变的，但我当时使用的函数并非由单独一个数字组成，而是由无限多个数字组成。

这个函数在物理上代表什么呢？使用函数而不是一个数字作为相变的序参量，是复本法是否奏效的分水岭。如果参数只有一个数字，复本法会导致荒谬的结果。相反，如果序参量是一个函数，即一组无穷多的数字（就像一条线可以被视为一组无穷多的点一样），那么复本法奏效，且会得到自洽的结果。

显然，如果需要用无穷多的数（即函数）来描述系统的相变，就必须有一个深刻的物理意义来支持，但这个意义在当时是完全无法理解的。

奇怪的数学

在开始讨论物理问题之前，我们先试着从数学角度来了解一下哪些改变是必要的。

为了使复本法有效，我必须对其进行“延拓”。某一数学方法存在延拓的可能性是基于一种古老的思想。第一个有这种想法的人可能是生活在14世纪中叶的法国主教、数学家、物理学家和经济学家尼古拉·德·奥雷姆。

这是一位令人难以置信的人物，他清楚地证明了中世纪并不像我们教科书中所说的那样是科学的黑暗时代。在能显示其才能的诸多证据中，有一本他写的书（大约在1360年！），讲的是大气折射造成的恒星位置的扭曲。我当然没有读完，因为是用拉丁语写的……然而，从概念的角度来看，他的推理是正确的。他可能是在日落时看到太阳在地平线上有被压扁的感觉而受到启发，认为这可能是一种扭曲变形现象。计算扭曲变形对于进行精确的天文观测是至关重要的，因为恒星的直接测量必须进行两到三度的校正。

回到我们的话题，奥雷姆第一个发现了一个数的1/2次幂就相当于它的平方根。现在对我们来说，这似乎微不足道，我们从高中就开始学了，却没有意识到奥雷姆在将幂的性质扩展到分数方面所做的逻辑飞跃，因为在他以前，幂的性质只适用于整数。

求幂的概念非常简单：求一个数的二次幂，就是取这个数两次，算出乘积；求三次幂，需要取三次，算出乘积，以此类推。所以求1/2次幂看起来显然是一个荒谬的操作，难道意味着“取半次”？奥雷姆的想法是将求幂的性质扩展，根据该性质，如果对一个已求幂的数求幂，则必须相应地把指数相乘。22的三次方等于26（即64，或为43）。

如果把一个数字平方后再求1/2次幂，我们会得到起始数字（因为2乘以1/2等于1），这意味着求1/2次幂相当于取平方根：事实上，一个数字平方后再取平方根就是该数字本身。

这些性质是正式推导出来的，因为取一个数字半次是没有意义的；然而，形式上确保了结果的自洽性。尼古拉·德·奥雷姆超越了最初的观点，即直接理解，而通过保存形式的一致性，他获得了一种非常简单的方法来解决极其复杂的运算。

从奥雷姆开始，数学经常在新的条件下以一种形式上正确的方式扩展性质，从而拓宽其适用范围。

为了解决我的问题，我使用了类似的方法。我在形式上应用了仅针对整数开发和验证的数学技术，希望形式上的性质对于非整数也仍然有效。

我的想法是组合数学的延伸。例如，组合数学告诉我有多少种方法可以将10个物体成对放置在5个抽屉中。扩展一下，我可以用同样的等式，算出在10个抽屉里放置5个物体的方式有多少种，这样每个抽屉里就有“半个”物体。显然，结果毫无意义，因为从实际的角度来看，操作无法完成，它并不对应于将物体一分为二，而只是说抽屉中物体的数量是二分之一。然而，为了得到一个正常的解（一般情况下处理的是真实的物体），我必须基于这些想象的物体来完成：抽屉里可以有半个物体，物体的总个数可以是非整数，把这些非整数的物体放进抽屉的方案数也可以是非整数！

从这个方法开始，我的想法是将物体分成两半，然后再分成两半，使抽屉中的物体数趋于零。

当然，这是一个纯粹的数学过程，几乎没有物理意义，但它得出了正确的结果，与模拟数据相符。

但是仍有两个问题悬而未决，即从数学上证明执行这种操作是有意义的，并从物理上理解用一个函数而不是单个变量来描述这个序参量的意义。

物理学解释

几年后，复本法的数学语言被翻译成了统计物理学的语言，尽管公式更为冗长，但却更容易理解。

通过一系列线索，我和我的朋友马克·梅扎尔、尼古拉·苏拉斯、热拉尔·图卢兹及米格尔·维拉索罗已经能够理解这一结果的物理意义，这是所有无序系统的共同特征，即无序系统同时处于大量不同的平衡态中。这是一个完全出乎意料的发现。

如图8所示，系统可以处于沿曲线分布的任何状态（例如，我们看图中四个黑点A、B、C、D，它们表示系统可以处于的许多可能性状态中的四个）。系统的各个状态都有不同的能量，且系统可以在不同的能量极小值处（凹陷处）达到平衡。在标为A的状态中，系统也处于该区域的最低点，状态B也一样，但在状态C和D中，系统处于较浅的凹陷（即系统处于平衡状态，除非升高系统温度，否则不会出离这一状态），但这不代表该区域的最小值。

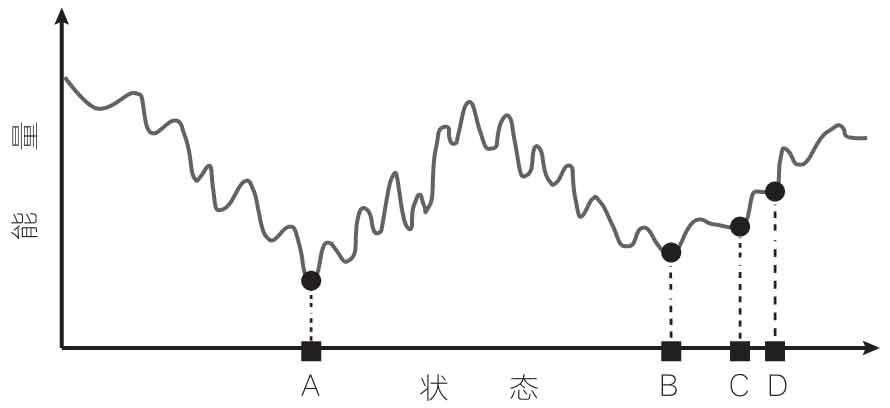
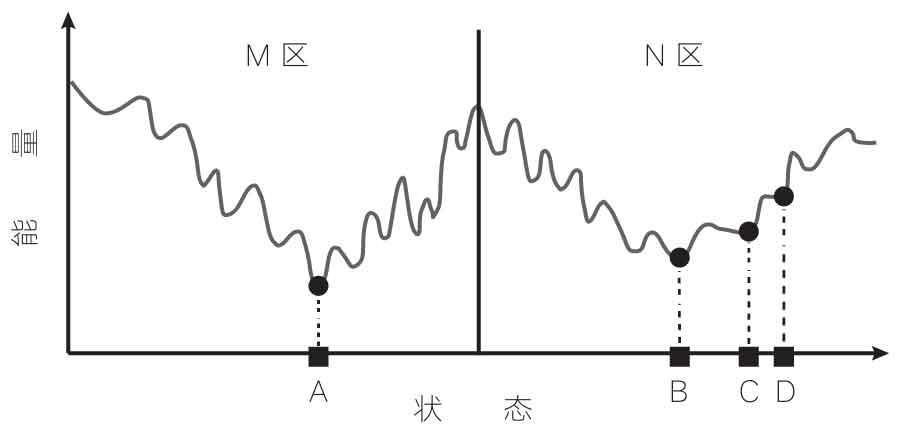
该图还显示了两个较大的凹陷区域（A周围的区域和B周围的区域），每个凹陷区域内都有许多小凹陷。我们可以称之为M区和N区（见图9）。当系统冷却到N区中的某个状态（例如B、C、D之中任何一个状态）时，即使温度升高，如果升高幅度不太大，系统也会保持在该区域。随后，系统将会在一个区域内不断演化，即发展为一系列构型，这些构型的选择是由系统的演化历史决定的，或者说是由其所处的区域决定的。在降温过程中，系统选择的区域只是众多可能性中的一个。

通常一个物理系统只处于一种状态。例如，在一定温度和压力下，水要么是液体，要么是固体，要么是气体。在某些特殊情况下，系统可能处于两种状态，我们通常称之为两种相。在100℃时，水可以同时处于液相和气相。也存在一个特殊的压力和温度值，此时水同时处于三种相：固相、液相和气相。这就是著名的水的“三相点”，它的出名并非偶然。一般来说，系统都会处于某个单一的相中。然而，我们也发现了同时处于无数相中的低温无序系统。这就是使用一个函数，即无穷多个数值的集合，来表示序参量的意义所在。

理解了这一点，对于物理学而言，是一个真正的进步。综合模型的建立及其结果让我们发现了一种从未见过的现象。就这样，无序系统的世界向我们敞开了大门。

从物理学的解释出发，数学解释也变成了可能。数学的论证花了二十多年时间，弗朗切斯科·圭拉及其合作者为了在一团乱麻中理清头绪做了很多基础工作。论证中使用的论据，就其简易性而言都颇具奇思妙想，但事后再看，这一切又似乎都很简单。

从模型到现实

为自旋玻璃的问题找到答案是研究真正玻璃的一个很好的起点，也就是研究那些镶在窗户上的玻璃，至今我们对其行为还没有一个完全的物理学认知。自20世纪90年代中期以来，我一直在断断续续地从事这项研究以获得准确的描述，从而使我们能够掌握玻璃相变的方方面面。

与自旋玻璃一样，真正的玻璃也是一个无序的系统，这种无序是由于玻璃的成分不仅有硅，还有许多杂质，以及许多不同类型、不同大小的分子，它们相互混合而构成玻璃。因此玻璃不能结晶，因为结晶需要规则的结构。如我们所见，被称为自旋玻璃的这种金属合金，其无序性是由金内部铁原子排列的随机性造成的，当金属是液体时，铁原子可以在金内部随机移动，但随着合金冷却，铁原子移动的可能性就越来越小，最后被随机困在某一位置。

现在，我们正试图对这个真实过程有一个具体的认识，一切看起来极其复杂，然而工作一旦完成，就会变得非常简单。当你在书上学习一个物理理论或数学定理时，不也是清晰明确的吗？然而为获得结果而进行的大量复杂工作却将灰飞烟灭。

另一个需要面对的有趣问题是从示意模型（例如刚刚讲解过的自旋玻璃模型）过渡到更为现实的模型，从而更详细地描述自旋之间的力，例如要考虑到自旋之间相互距离的因素。

相变是通过具有精确空间位置的个体之间的相互作用而发生的，这在前面讨论时用的简化模型中没办法呈现。

除了缺乏空间结构外，简化模型也无法呈现时间的发展。

当我们要研究的系统处于平衡状态时，也就是说当它在某一时段内保持稳定时，统计力学的技术就“容易”派上用场。对于玻璃或蜡等无序系统，达到平衡状态所需的时间通常非常长，可能要好几年或好几个世纪。当然这也会发生在窗户的玻璃上，只不过我们会用一些工业技术让它们更加坚固。

如果一个物理过程不处于平衡状态，那么时间就有了意义，因为人们总是可以区分过程的时间前后，这在处于平衡状态的系统中是无法区分的。

简单地说，如果一个球处于稳定的平衡状态，即停在坑底，给它拍一些照片，那么我们永远无法将这些照片按拍摄的时间顺序排列，因为这个球的状态未呈现出任何变化的迹象。但是，如果拍摄一个滚落的球，情况就会发生变化，因为在不平衡的状态下，时间先后是显而易见的。

因此，我们面临的问题是要将理论拓展至和时间相关的情形，因为存在这种不平衡状态；另外，我们还要将理论拓展至和空间相关的情形，因为这些过程都在空间中进行，而且只有相邻粒子之间才会有相互作用。总之，为了彻底了解玻璃的相变，还有大量的工作要做。

拓宽视野

我的初衷是检查一种可以帮我解决粒子问题的数学方法（对于那个问题，复本法的原始版本得心应手），后来我发现自己掌握了一个非常强大而实用的数学和概念工具，可用于解决各种貌似毫无关联的问题，也就是与无序系统相关的问题。

现实世界是混乱无序的，正如我们一开始所说的那样，许多现实世界的情况可以通过大量相互作用的基本单元来描述。

我们可以用简单的规则将单元之间的相互作用模式化，但这些集体行为的结果实在是难以预料。

所谓基本单元一般是自旋、原子或分子、神经元、细胞，但也包括网站、证券经纪人、股票和债券、人、动物、生态系统的各个组成部分……

并非所有基本单元之间的相互作用都会产生无序系统。无序产生的原因是一些基本单元的行为与众不同，比方说一些自旋试图反向排列，一些原子与其他大多数原子有区别，个别金融运营商抛售其他人正在购买的股票，一些受邀参加晚宴的嘉宾与某些客人不睦，想坐得离他们远点……

这样看来，在所有这些无序的情况下，我发现的数学和概念工具对于解决问题都是不可或缺的。

例如，最近我们做了一个实验，将尽可能多的大小不一的固体小球放入一个盒子中，结果实验取得了重要的成果。这是一个非常有趣的问题，因为这些大小不一的固体小球可以用来构建液体、晶体、胶体系统、颗粒系统和粉末的模型。此外，固体小球的“装箱问题”与信息和优化理论的重要问题也息息相关。

在巨人的肩膀上

伽利略·伽利莱发现了一个非常强大的研究自然的工具，就是将自然现象简化。他建立了一个完全忽略摩擦的理论，请注意，在一个没有摩擦的世界里，我们既不能走路（因为会滑倒），也不能吃饭（因为食物会从餐具上掉下来）。现代物理学肇始于伽利略的世界，与真实世界截然不同。在后来的几个世纪里，这个世界有其他元素被添加进来，使之成为令人满意的对真实世界的近似描述。埃万杰利斯塔·托里拆利在一封信中有一段关于物体运动的文字非常优美，很好地诠释了伽利略的这一观点：

“《论运动》学说的原理是真是假，对我来说无关紧要。因为，如果它们不是真的，我们可以根据我们的假设来假装是真的，然后获得从这些原理推导出来的所有推论，不是模棱两可的，而是纯粹而严谨的。我想象或假设某个物体或某一点以一定的比例上下运动，在水平方向也做同样的运动（翻译成现代语言，就是‘在没有大气摩擦的情况下移动’）。在这种情况下，我认为一切就会遵循伽利略提出的理论，还有我的理论。如果铅球、铁球、石球不遵守这个假设的比例，会由于摩擦而减速，那我们会说，我们讨论的对象不是这些球本身。”

然而，对于托里拆利这位有着同样丰富经验的实验物理学家而言，理解物体在没有摩擦情况下的运动显然是理解有摩擦现象的前提，当然也是必不可少的一步。

几百年来，人们以将物理现象简化为本质的能力为肇端，不断推动物理学的发展。时至今日，物理学已变得如此博大精深，以至于可以将复杂性和无序性重新引入模型中，而这正是当年伽利略不得不放弃的东西。