1

下面接着上一篇关于学习的话题讲讲。先从我刚才翻译的那篇文章中出现的人名和书名讲起。其实讲这些只是为了说明我小时候采用的学习方法。大家现在只要记住有一位叫作柏拉图的古希腊哲学家——他活跃在公元前五世纪末到公元前四世纪中叶，曾在雅典创办学校（阿卡德米，即雅典学院），是苏格拉底[苏格拉底（前469—前330），著名的古希腊哲学家，他和他的学生柏拉图及柏拉图的学生亚里士多德被并称为“古希腊三贤”。他一生没留下任何著作，但影响巨大，被普遍认为是西方哲学的奠基者。他的哲学主要研究探讨的是伦理道德问题。]的学生。将来大家进大学后如果能想起来这个名字，我希望大家能读几本他写的《柏拉图对话录》。[《柏拉图对话录》既是哲学名著，又是文学名著。记录了苏格拉底和学生的对话。]

这就是我学习的方法。我发明这种一个人也能学习的方法是在十岁的时候——父亲去世后，我没有可以直接问问题的人了。直到现在，我仍在使用这种学习方法。

其证据就是，今天我要为给大家讲课做一些准备。在开始准备之前，即便什么都没看，我脑子里也会立刻浮现出一些想法来。但我还是要查阅一下自己的卡片盒，这些卡片盒现在已有钢琴那么高了，我查阅了“教育”分类部分。从原理上讲，这种卡片和我小时候没有分类地在本子上记东西是一样的。

卡片上记录了我前段时间看过的、觉得蛮有意思的诺斯洛普·弗莱1著作的书名，以及其中有关教育论述的具体页数。我又去二楼的书库，找到了弗莱的这本书。我在阅读时，曾在书上自己觉得重要的句子下面画过红线，写过眉批，此时都起作用了。

1诺斯洛普·弗莱（1912—1991），加拿大文学批评家。 接下来我要做的，是从《柏拉图全集》中找出收入了《枚农》的那一卷来，确认一下弗莱引用的部分是否正确。

由于我要在大家面前讲课，我就特别注意到了下面这一点。《柏拉图对话录》采用的是记录他的老师苏格拉底与其他人的对话的形式写成的。这正是非常典型的、弗莱所说的那种老师比学生多提问的对话。苏格拉底之所以这样做，是为了要把学生没有用语言表达、心里却很清楚的想法引导出来。

《枚农》写的是一位对于雅典人来说，来自别的国家的、名叫枚农的年轻人和苏格拉底的对话。现在在我国，人们对应该如何进行道德教育进行了很多讨论。比如“为什么不能杀人？”“作为个人自我的私，与政府的方针、国家的发展（写作‘公’，日语读音是‘OYAKE’），哪一方更为重要？”等等。

应该说你们这些学生是最辛苦的，因为你们还必须接受这方面的教育，不过，刚才说的一般意义上的“道德”，与这本《枚农》所谈论的“德”有所不同。

我希望大家记住《枚农》这本书（岩波文库也有），希望大家进大学后也能读一下。小时候，当我遇到读了也不能完全理解、打算以后什么时候再读的书时，就把作者和书名记在本子上，还写上为什么将来想要读它，以及自己那个年龄所能理解的、最感兴趣的部分等等。尽管更多的是将自己觉得有意思的一段话摘抄下来……

过了几年以后，我真的读了那本书，确认了和原来想的一样是一本好书时，我会异常高兴的。在棒球比赛中不是有“击中”这个用语吗？书和读者之间也有这种“击中”的关系。读书的能力（在成长期，与年龄很有关系），为了读这本书而进行的预备阅读，以及生活阅历，都会帮助我“击中”。

同样，如果你们想要“击中”某本书，先不要急于开始阅读。并且，你要经常注意发现自己不知道的书。觉得这有可能是一本好书时，最好先去书店或图书馆读一读这本书。如果有富余的钱，就把它买下来，以后不要忘记它，直到有一天你朝着那本书走去，如同走向棒球的击球区。

2

为了让大家记住《枚农》这本书，我讲一下其中特别有趣味的部分吧。对于你们当中学过初等几何的人来说，是很容易懂的。我在新制中学学习的时候，从那些在韩国境内的旧制高中学习过的年轻人手中，得到了他们使用过的各种课本。战败后，他们马上就回到了日本，因为原来那个学校已经不再是日本人的学校了。由于几何入门书可以自己学习，我就很投入地学起来。

苏格拉底认为，有些知识，人不用学也是知道的，在柏拉图学说中，这也是一个重要的思想，但不在这里讲了。为了证明这一点，在刚才提到的对话中，苏格拉底把枚农的年轻仆人喊过来，围绕着几何图形和他进行了对话。苏格拉底首先在地上画了一个正方形ABCD（由此可以知道，这是在户外边走边进行的对话），对话是有关学习哲学的方法的。

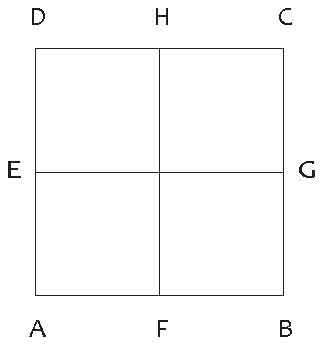
然后，苏格拉底将四条边的中点两两相连，分别画出EG、HF两条线（见图一），按照古希腊的度量法，设AB的长度为二布斯——法语旧制长度单位中，皮埃[即法尺pied。]（原意是脚）的十二分之一是普斯[即法寸puce。]，差不多有一英寸长，可以把布斯看做和普斯大体相等。然后问那少年，这个正方形的面积是多少？那少年回答是四平方布斯后，他又问道，这图形的二倍是多大？少年回答当然是八平方布斯。苏格拉底接着又问，那么那个图形的边长是多少布斯呢？少年回答说：

“这很简单，苏格拉底，当然是原来边长的两倍了。”（岩波书店《柏拉图全集》）

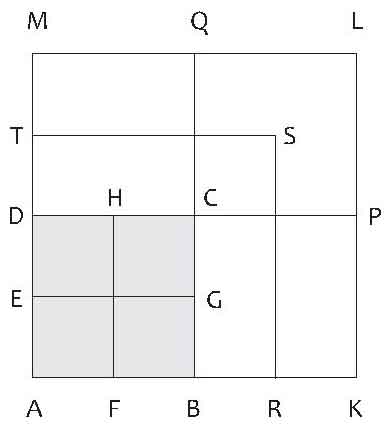
但少年的回答是错的。于是苏格拉底又画了一个图（见图二），还在其中画了一个ATSR的边长三布斯的图形，继续向少年提问，好让他认识到自己的错误。“你看，这个AKLM正方形的面积，是原来那个图形的四倍吧。”苏格拉底对少年说，“你用手指一下，原来图形两倍面积的正方形的边长是哪个，说不出数字来也没有关系。”

少年回答说：“我不知道，我对宙斯发誓，苏格拉底，我实在弄不明白。”

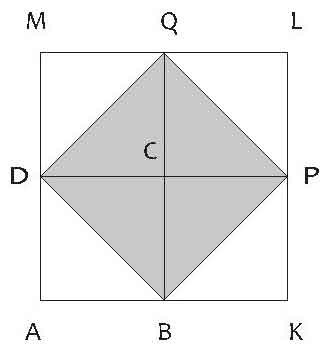
于是，苏格拉底又将AKLM图形进一步简化（见图三），然后，在上面画出了DB——学者们称之为图形ABCD的对角线。这是为了让那少年明白，把DB作为一个边的话，可形成该图形面积的二分之一的正方形。这一点，少年用自己的眼睛看图就已经理解了。由于这个BDQP图形是AKLM的二分之一，所以是最初图形ABCD的面积的两倍，即苏格拉底提问的数字。

以这个几何题为例子，《枚农》要证明的是柏拉图关注的一个中心问题，翻译过来，即“想起”[希腊语anamnesis。柏拉图认为，人的灵魂是不朽的。所以，一个人的知识常常在他成为一个人之前已经具有了，教育只是“使知识从内部成长”，这成长的过程即“被提醒、回忆的过程”。[参见《柏拉图——生平及其著作》,山东人民出版社，1991年，（英）A．E.泰勒著，谢随知等译。]]。对这个词语的理解有待于你们将来去“击中”了。

我想说的是，即便是古典哲学，如果在儿童时代听到的是轻松愉快的讲解，一般是不会忘记的，这一点很重要。你们长大后，它会和你们的学习，以至做学问连接起来的。我深刻感受到，当年在四国的森林中，自己为读书所做的笔记和学习方法一直延续到了现在，才有了今天的我。

3

我并不是说对自己的教育有多成功，也不是满足于现在的自己。事实上我发现，用自己的方法进行的以读书为中心的自我教育中，存在着许许多多的漏洞。为了多少填补一下这些漏洞，我每天都在努力。特别是快六十岁时，我曾一度停止写小说，想重新开始读书。我不知道自己还能活多少年，也许这辈子也不能全部填补上。

我只是想从个人的经验出发告诉大家，从小时候开始的为了自己的学习是可以不间断地持续一生的。我还想告诉大家，小时候想到的“我就要这样生活”，并以自己的方式开始的生活是可以持续一生的。在此必须加上一句，如果自己认为另一个方向更好的话，也是可以进行修正的。

这里所说的“持续”很重要。在我留给大家的作业中，写到了这个问题。在那篇文章中，我写了母亲曾经说过的话：“去学校学习，是为了将那些没能长大就死去的孩子知道的语言以及他们的全部，都在自己这里继续下去。”因此，也可以说成是“继续”。以自己的意愿去“持续”就是“继续”。自己去替代那些没能长大就死去的孩子也是“继续”的一种。

多年以来，我一直是在为沿着自己小时候选择的道路继续走下去而学习、工作的。虽然这样说，小时候的我却以为，长大以后，自己会成为一个完全不同的人。因为小时候，在我眼里，大人们很有大人样，和孩子是完全不一样的人。

不过，我现在已经长成大人了，这把年纪都算得上是老人了。我刚才讲到的柏拉图的《枚农》的对话发生于苏格拉底去世前三年，也就是说，记录的是苏格拉底六十七岁时的对话，大致是我现在这个年龄。到了这个年龄，我彻底弄明白了一件事：不管怎么说，大人和孩子之间是一种延续的、连接的关系。如果要问我想对半个世纪前的自己说些什么，这就是我能够告诉他的最大秘密。

还有一句话想跟你们说，如果认为自己到现在为止的生活方式是错的，那就应该换一种活法，而不是一死了之。这一点我刚才讲过有多么重要了。虽说做起来有点难，但这也是在发现自己的新的连接。

基本上，对大多数人来说，从小到老，自己内心世界里的“人”是连接着、持续着的。而且，在自己心中的这个“人”，是和日本人以及整个人类的历史连接在一起的。这一点是我母亲教给我的。

这就是说，从未来的角度看，当大家长成大人之后，那时的你们和现在你们心中的“人”是相连接的，也是和未来的日本人、全人类相连接的。所以，大家一定要珍视自己内心的“人”。这就是我最想跟大家讲的话。